
分析 设各人上场时间分别为7t1,7t2,7t3,7t4,13t5,13t6,13t7,(ti为正整数)得方程 7(t1+t2+t3+t4)+13(t5+t6+t7)=90×3.令t1+t2+t3+t4=x,t5+t6+t7=y,得方程7x+13y=270.即求此方程满足4≤x≤38,3≤y≤20的整数解,再根据分类和分步计数原理可得答案.
解答 解:设各人上场时间分别为7t1,7t2,7t3,7t4,13t5,13t6,13t7,(ti为正整数).
得方程 7(t1+t2+t3+t4)+13(t5+t6+t7)=90×3.
令t1+t2+t3+t4=x,t5+t6+t7=y,得方程7x+13y=270.即求此方程满足4≤x≤38,3≤y≤20的整数解.
即6y≡4(mod 7),3y≡2(mod 7),y≡3(mod 7)
∴y=3,10,17,相应的x=33,20,7.
t5+t6+t7=3的解只有1种,t5+t6+t7=10的解有C92种,t5+t6+t7=17的解有C162种;
t1+t2+t3+t4=33的解有C323种,t1+t2+t3+t4=20的解有C193种,
t1+t2+t3+t4=7的解有C63种.
∴共有1×C323+C63×C162×+C193×C92=42244种.
点评 本题考查了分步分类计数原理,本题转化为方程7x+13y=270.即求此方程满足4≤x≤38,3≤y≤20的整数解是关键,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
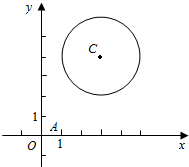 已知圆C:ABCD,直线l1过定点A (1,0).
已知圆C:ABCD,直线l1过定点A (1,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥$\frac{1}{2}$ | B. | m≥2 | C. | 0<m<2 | D. | 0<m<$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com