
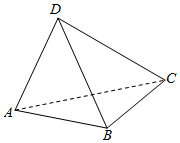
 如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.
如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2. 分析 由已知得$\overrightarrow{AC}$=$\overrightarrow{a}-\overrightarrow{c}$,$\overrightarrow{BD}$=$\overrightarrow{b}+\overrightarrow{c}$,从而由$\overrightarrow{AC}•\overrightarrow{BD}$=($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}+\overrightarrow{c}$)=-3,得|($\overrightarrow{a}-\overrightarrow{b}$)-$\overrightarrow{c}$|=2,从而$\frac{c^2}{ab+1}$=$\frac{\overrightarrow{a}•\overrightarrow{b}+(\overrightarrow{a}-\overrightarrow{b})\overrightarrow{c}+3}{\overrightarrow{a}•\overrightarrow{b}+1}$,由此入手能求出$\frac{c^2}{ab+1}$的最小值.
解答 解:∵在三棱锥D-ABC中,AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$
∴$\overrightarrow{AC}$=$\overrightarrow{a}-\overrightarrow{c}$,$\overrightarrow{BD}$=$\overrightarrow{b}+\overrightarrow{c}$,
∴$\overrightarrow{AC}•\overrightarrow{BD}$=($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}+\overrightarrow{c}$)
=$\overrightarrow{a}•\overrightarrow{b}+\overrightarrow{a}•\overrightarrow{c}-\overrightarrow{b}•\overrightarrow{c}-{\overrightarrow{c}}^{2}$=-3,
∴${\overrightarrow{c}}^{2}$=$\overrightarrow{a}•\overrightarrow{b}$+$\overrightarrow{a}•\overrightarrow{c}$-$\overrightarrow{b}•\overrightarrow{c}$+3,
又$\overrightarrow{AB}$=$\overrightarrow{a}-\overrightarrow{BD}$=$\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}$,
∴|($\overrightarrow{a}-\overrightarrow{b}$)-$\overrightarrow{c}$|=2,①
∴$\frac{c^2}{ab+1}$=$\frac{\overrightarrow{a}•\overrightarrow{b}+(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{c}+3}{ab+1}$,②
将①两边平方得$(\overrightarrow{a}-\overrightarrow{b})^{2}+{\overrightarrow{c}}^{2}-2(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{c}=4$,
∴$(\overrightarrow{a}-\overrightarrow{b})^{2}+{\overrightarrow{c}}^{2}-4=2(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{c}$,
∴$\frac{(\overrightarrow{a}-\overrightarrow{b})^{2}}{2}+\frac{{\overrightarrow{c}}^{2}}{2}-2=(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{c}$,
代入②中,得$\frac{{c}^{2}}{\overrightarrow{a}•\overrightarrow{b}+1}$=$\frac{\overrightarrow{a}•\overrightarrow{b}+\frac{(\overrightarrow{a}-\overrightarrow{b})^{2}}{2}+\frac{{\overrightarrow{c}}^{2}}{2}+1}{ab+1}$,
∴$\frac{1}{2}{\overrightarrow{c}}^{2}$=$\overrightarrow{a}•\overrightarrow{b}$+1+$\frac{(\overrightarrow{a}-\overrightarrow{b})^{2}}{2}$
=$\overrightarrow{a}•\overrightarrow{b}+1+\frac{1}{2}({\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b})$
=1+$\frac{1}{2}$(${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$),
∴${\overrightarrow{c}}^{2}=2+{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$,
又${\overrightarrow{{c}^{\;}}}^{2}$=c2,${\overrightarrow{a}}^{2}={a}^{2}$,${\overrightarrow{b}}^{2}={b}^{2}$,
∴$\frac{c^2}{ab+1}$=$\frac{2+{a}^{2}+{b}^{2}}{ab+1}$≥$\frac{2+2ab}{ab+1}$=2.
∴$\frac{c^2}{ab+1}$的最小值为2.
故答案为:2.
点评 本题考查三角形中关于边长的代数式的最小值的求法,是中档题,解题时要认真审题,注意向量知识的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 671 | B. | 672 | C. | 673 | D. | 674 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com