
【题目】如图,在三棱柱![]() 中,四边形
中,四边形![]() 是菱形,四边形
是菱形,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
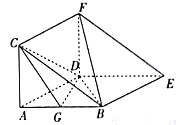
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)(1)连接AF,与CD交于点H,连接GH,易得BF∥GH,从而得证;
(2)以D为原点,直线DG,DE,DF分别为x轴,y轴,z轴建立空间直角坐标系,通过求面BCD的一个法向量为![]() 和面BEF的一个法向量为
和面BEF的一个法向量为![]() ,利用
,利用![]() =
=![]() 即可得解.
即可得解.
(1)连接AF,与CD交于点H,连接GH,
则GH为△ABF的中位线,
所以BF∥GH,
又BF![]() 平面CDG,GH平面CDG,
平面CDG,GH平面CDG,
所以BF∥平面CDG.

(2)由题意可知,直线DG,DE,DF两两垂直,
以D为原点,直线DG,DE,DF分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面BCD的一个法向量为![]() =
=![]() ,则有
,则有 ,得
,得 ,
,
取![]() ,得,所以
,得,所以![]() =
=![]() ,
,
设平面BEF的一个法向量为![]() =
=![]() ,则有
,则有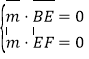 ,得
,得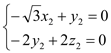 ,
,
取![]() ,得
,得![]() ,所以
,所以![]() =
=![]() ,
,
设平面BCD与平面BEF所成锐二面角为![]()
则![]() =
= ,
,
所以平面BCD与平面BEF所成锐二面角的余弦值为![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】某中学将要举行校园歌手大赛,现有4男3女参加,需要安排他们的出场顺序.(结果用数字作答)
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果女生甲在女生乙的前面(可以不相邻),那么有多少种不同的出场顺序?
(3)如果3位女生都相邻,且女生甲不在第一个出场,那么有多少种不同的出场顺序?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两条互相垂直的直线都经过原点(两条直线与坐标轴都不重合)且与曲线![]() 分别交于点
分别交于点![]() (异于原点),且
(异于原点),且![]() ,求这两条直线的直角坐标方程.
,求这两条直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .

(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名?
(3)已知![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国有个名人叫做布莱尔·帕斯卡,他认识两个赌徒,这两个赌徒向他提出一个问题,他们说,他们下赌金之后,约定谁先赢满5局,谁就获得全部赌金700法郎,赌了半天,甲赢了4局,乙赢了3局,时间很晚了,他们都不想再赌下去了.假设每局两赌徒输赢的概率各占![]() ,每局输赢相互独立,那么这700法郎如何分配比较合理( )
,每局输赢相互独立,那么这700法郎如何分配比较合理( )
A.甲400法郎,乙300法郎B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎D.甲350法郎,乙350法郎
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张矩形白纸![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,现分别将
的中点,现分别将![]() 沿
沿![]() 折起,且点
折起,且点![]() ,
,![]() 在平面
在平面![]() 同侧,则下列命题正确的是______(写出所有正确命题的序号)
同侧,则下列命题正确的是______(写出所有正确命题的序号)

①当平面![]() //平面
//平面![]() 时,
时,![]() //平面
//平面![]() ;
;
②当平面![]() //平面
//平面![]() 时,
时,![]() //
//![]() ;
;
③当![]() ,
,![]() 重合于点
重合于点![]() 时,
时,![]() ;
;
④当![]() ,
,![]() 重合于点
重合于点![]() 时,三棱锥
时,三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com