
分析 (1)利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,x∈[$\frac{π}{4}$,$\frac{π}{2}$].求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最小值.
(2)根据f(x)=$\frac{3}{2}$的值;构造f(x-$\frac{π}{6}$)的关系式,即可求值.
解答 解:函数f(x)=2sin2(x+$\frac{π}{4}$)-$\sqrt{3}$cos2x-1,
化简可得:f(x)=1-cos(2x+$\frac{π}{2}$)-$\sqrt{3}$cos2x-1
=1+sin2x-$\sqrt{3}$cos2x-1
=2sin(2x-$\frac{π}{3}$)
∵x∈[$\frac{π}{4}$,$\frac{π}{2}$].
∴2x-$\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{2π}{3}$].
∴sin(2x-$\frac{π}{3}$)∈[$\frac{1}{2}$,1]
2sin(2x-$\frac{π}{3}$)∈[1,2]
故得f(x)的最小值为1.
(2)由(1)知f(x)=2sin(2x-$\frac{π}{3}$),
可得:f(x-$\frac{π}{6}$)=2sin(2x-$\frac{2π}{3}$)=2sin(2x-$\frac{π}{3}-\frac{π}{3}$)=2sin(2x-$\frac{π}{3}$)cos$\frac{π}{3}$-2cos(2x-$\frac{π}{3}$)sin$\frac{π}{3}$.
∵f(x)=$\frac{3}{2}$,即2sin(2x-$\frac{π}{3}$)=$\frac{3}{2}$,
可得:sin(2x-$\frac{π}{3}$)=$\frac{3}{4}$$<\frac{2\sqrt{3}}{4}$,
即2x-$\frac{π}{3}$$<\frac{π}{3}$,
∴cos(2x-$\frac{π}{3}$)=$\frac{\sqrt{7}}{4}$,
那么:f(x-$\frac{π}{6}$)=$2×\frac{3}{4}×\frac{1}{2}-2×\frac{\sqrt{7}}{4}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{21}+3}{4}$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,ex>0”的否定是“?x∈R,使ex>0” | |
| B. | 若x+y≠3(x,y∈R),则x≠2或y≠1 | |
| C. | “x2+2x≥ax(1≤x≤2)恒成立”等价于“(x2+2x)min≥(ax)max(1≤x≤2)” | |
| D. | “若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{{π}^{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
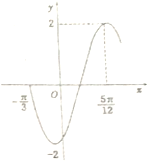 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )| A. | y=2sin(2x-$\frac{π}{6}$) | B. | y=2sin(2x+$\frac{π}{6}$) | C. | y=2sin(2x) | D. | y=2sin(2x+$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
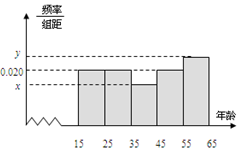 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.20 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65] | 20 | 0.40 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com