考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:对第①问,由题干条件及椭圆定义,得a,将点A的坐标代入椭圆方程中,得b2,从而得椭圆的方程;
对第②问,设动点K(x0,y0),设F1K的中点为M(x,y),用x,y分别表示x0,y0,再将坐标(x0,y0)代入椭圆方程中,即得动点M的轨迹方程.
解答:
解:①由椭圆的定义知,|AF
1|+|AF
2|=2a,即4=2a,得a
2=4,
从而椭圆C的方程可写成
+=1.
将A的坐标
(1,)代入上式中,得
+=1,得b
2=3,
所以椭圆C的方程为
+=1.
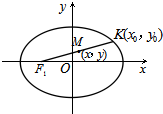
②由①知,F
1的坐标为(-1,0),设动点K(x
0,y
0),线段F
1K的中点为M(x,y),如右图所示.
则由中点公式,有
,变形为
,
将上式代入
+=1中,得
+=1,
即得线段F
1K中点的轨迹方程为
(x+)2+=1.
点评:本题考查了椭圆的方程,椭圆的定义,轨迹方程的求法,利用相关点法求轨迹方程的一般步骤是:
(1)设轨迹上的点为M(x,y),其他点(即相关点)设为(x0,y0),(x1,y1),(x2,y2)等;
(2)寻找x,y与相关点的关系,用x,y表示相关点;
(3)将相关点的坐标代入曲线方程中,化简,整理,即得动点M的轨迹方程.



