练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在锐角三角形ABC中，求证：sinA＋sinB＋sinC>cosA＋cosB＋cosC.

     

    见解析

    【解析】证明：∵△ABC为锐角三角形，

    ∴A＋B>，∴A>－B，

    ∵y＝sinx在(0，)上是增函数，

    ∴sinA>sin(－B)＝cosB，

    同理可得sinB>cosC，sinC>cosA，

    ∴sinA＋sinB＋sinC>cosA＋cosB＋cosC.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-4直线、平面平行的判定及性质（解析版） 题型：填空题

    对于平面M与平面N，有下列条件：①M，N都垂直于平面Q；②M、N都平行于平面Q；③M内不共线的三点到N的距离相等；④l，m为两条平行直线，且l∥M，m∥N；⑤l，m是异面直线，且l∥M，m∥M；l∥N，m∥N，则可判定平面M与平面N平行的条件是________(填正确结论的序号)．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-7数学归纳法（解析版） 题型：解答题

    用数学归纳法证明42n＋1＋3n＋2能被13整除，其中n∈N*.

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：填空题

    若a，b，c是不全相等的正数，给出下列判断：

    ①(a－b)2＋(b－c)2＋(c－a)2≠0；

    ②a>b与a<b及a＝b中至少有一个成立；

    ③a≠c，b≠c，a≠b不能同时成立．

    其中判断正确的是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：选择题

    若P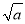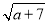＝＋，Q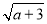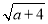＝＋ (a≥0)，则P，Q的大小关系(　　)

    A．P>Q B．P＝Q

    C．P<Q D．由a取值决定

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-5合情推理与演绎推理（解析版） 题型：选择题

    观察下列各式：a＋b＝1，a2＋b2＝3，a3＋b3＝4，a4＋b4＝7，a5＋b5＝11，…，则a10＋b10＝(　　)

    A. 28 B. 76 C. 123 D. 199

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：解答题

    已知lg(3x)＋lgy＝lg(x＋y＋1)．

    (1)求xy的最小值；

    (2)求x＋y的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-2一元二次不等式及其解法（解析版） 题型：解答题

    设a≠0，对于函数f(x)＝log3(ax2－x＋a)，

    (1)若函数f(x)的定义域为R，求实数a的取值范围；

    (2)若函数f(x)的值域为R，求实数a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-4数列求和（解析版） 题型：填空题

    在数列{an}中，a1＝2，an＋an＋1＝1(n∈N*)，设Sn为数列{an}的前n项和，则S2007－2S2006＋S2005的值为________．

     

    查看答案和解析>>

    同步练习册答案