练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知lg(3x)＋lgy＝lg(x＋y＋1)．

    (1)求xy的最小值；

    (2)求x＋y的最小值．

     

    （1）1 （2）2

    【解析】【解析】
    由lg(3x)＋lgy＝lg(x＋y＋1)得

    (1)∵x>0，y>0，

    ∴3xy＝x＋y＋1≥2＋1，

    ∴3xy－2－1≥0，

    即3()2－2－1≥0，

    ∴(3＋1)(－1)≥0，

    ∴≥1，∴xy≥1，

    当且仅当x＝y＝1时，等号成立．

    ∴xy的最小值为1.

    (2)∵x>0，y>0，

    ∴x＋y＋1＝3xy≤3·()2，

    ∴3(x＋y)2－4(x＋y)－4≥0，

    ∴[3(x＋y)＋2][(x＋y)－2]≥0，

    ∴x＋y≥2，

    当且仅当x＝y＝1时取等号，

    ∴x＋y的最小值为2.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：解答题

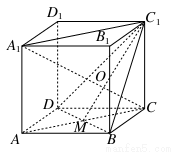
    如图所示，正方体ABCD－A1B1C1D1中，A1C与截面DBC1交于O点，AC，BD交于M点，求证：C1，O，M三点共线．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：选择题

    若a，b∈R，则下面四个式子中恒成立的是(　　)

    A．lg(1＋a2)>0 B．a2＋b2≥2(a－b－1)

    C．a2＋3ab>2b2 D. <

     

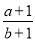
    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-5合情推理与演绎推理（解析版） 题型：解答题

    在锐角三角形ABC中，求证：sinA＋sinB＋sinC>cosA＋cosB＋cosC.

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-5合情推理与演绎推理（解析版） 题型：选择题

    三段论推理“①矩形是平行四边形；②三角形不是平行四边形；③三角形不是矩形”中的小前提是(　　)

    A．① B．② C．③ D．①和②

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：选择题

    设x，y∈R，a>1，b>1，若ax＝by＝2，a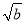＋＝4，则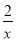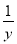＋的最大值为(　　)

    A．4 B．3 C．2 D．1

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-2一元二次不等式及其解法（解析版） 题型：解答题

    已知不等式ax2＋bx＋c>0的解集为(1，t)，记函数f(x)＝ax2＋(a－b)x－c.

    (1)求证：函数y＝f(x)必有两个不同的零点；

    (2)若函数y＝f(x)的两个零点分别为m，n，求|m－n|的取值范围；

    (3)是否存在这样的实数a，b，c及t使得函数y＝f(x)在[－2,1]上的值域为[－6,12]？若存在，求出t的值及函数y＝f(x)的解析式；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-1不等关系与不等式（解析版） 题型：填空题

    已知1≤lg(xy)≤4，－1≤lg≤2，则lg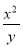的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-4数列求和（解析版） 题型：选择题

    若数列{an}为等比数列，且a1＝1，q＝2，则Tn 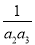＝＋＋…＋的结果可化为(　　)

    A．1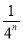－ B．1－

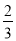    C．(1－) D． (1－)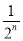

     

    查看答案和解析>>

    同步练习册答案