
若数列{an}为等比数列,且a1=1,q=2,则Tn = +
+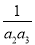 +…+
+…+ 的结果可化为( )
的结果可化为( )
A.1-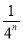 B.1-
B.1-
C. (1-
(1- ) D.
) D.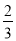 (1-
(1-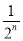 )
)
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:解答题
已知lg(3x)+lgy=lg(x+y+1).
(1)求xy的最小值;
(2)求x+y的最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:选择题
已知a<0,-1<b<0,那么下列不等式成立的是( )
A.a>ab>ab2 B.ab2>ab>a
C.ab>a>ab2 D.ab>ab2>a
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:填空题
在数列{an}中,a1=2,an+an+1=1(n∈N*),设Sn为数列{an}的前n项和,则S2007-2S2006+S2005的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:填空题
设数列{an}的首项a1=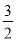 ,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足
,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足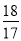 <
<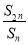 <
<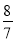 的所有n的和为________.
的所有n的和为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:解答题
已知首项为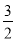 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-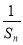 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:选择题
设等比数列{an}的前n项和为Sn,若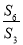 =3,则
=3,则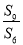 =( )
=( )
A.2 B.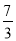 C.
C.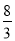 D.3
D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-1数列的概念与简单表示法(解析版) 题型:解答题
设数列{an}的前n项和Sn满足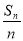 =3n-2.
=3n-2.
(1)求数列{an}的通项公式;
(2)设bn=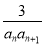 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<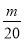 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:选择题
已知平面向量a,b,|a|=1,|b|=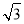 ,且|2a+b|=
,且|2a+b|=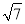 ,则向量a与向量a+b的夹角为( )
,则向量a与向量a+b的夹角为( )
A.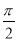 B.
B. C.
C.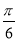 D.π
D.π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com