
已知首项为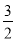 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-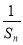 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
(1)an=(-1)n-1·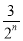 .
.
(2)最大项的值为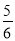 ,最小项的值为-
,最小项的值为-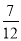 .
.
【解析】【解析】
(1)设等比数列{an}的公比为q,
∵S3+a3,S5+a5,S4+a4成等差数列,
∴S5+a5-S3-a3=S4+a4-S5-a5,
即4a5=a3,
于是q2=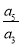 =
=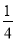 .
.
又{an}不是递减数列且a1=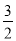 ,∴q=-
,∴q=-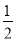 .
.
故等比数列{an}的通项公式为an=(-1)n-1·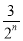 .
.
(2)由(1)得Sn=1-(-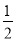 )n=
)n=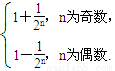
当n为奇数时,Sn随n的增大而减小,
∴1<Sn≤S1=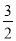 ,
,
故0<Sn-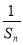 ≤S1-
≤S1-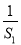 =
=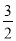 -
-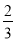 =
=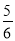 .
.
当n为偶数时,Sn随n的增大而增大,
∴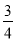 =S2≤Sn<1,
=S2≤Sn<1,
故0>Sn-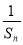 ≥S2-
≥S2-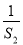 =
=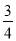 -
-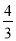 =-
=- .
.
综上,对于n∈N*,总有-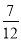 ≤Sn-
≤Sn- ≤
≤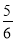 .
.
∴数列{Tn}最大项的值为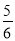 ,最小项的值为-
,最小项的值为-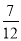 .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:选择题
设x,y∈R,a>1,b>1,若ax=by=2,a+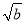 =4,则
=4,则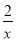 +
+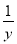 的最大值为( )
的最大值为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-5数列的综合应用(解析版) 题型:填空题
定义:称 为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为
为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为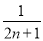 ,则数列{cn}的通项公式为cn=________.
,则数列{cn}的通项公式为cn=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:填空题
若数列{an}是正项数列,且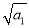 +
+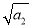 +…+
+…+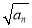 =n2+3n(n∈N*),则
=n2+3n(n∈N*),则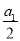 +
+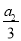 +…+
+…+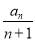 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:选择题
若数列{an}为等比数列,且a1=1,q=2,则Tn = +
+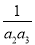 +…+
+…+ 的结果可化为( )
的结果可化为( )
A.1-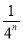 B.1-
B.1-
C. (1-
(1- ) D.
) D.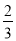 (1-
(1-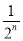 )
)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:选择题
等比数列{an}的前n项和为Sn,若a1+a2+a3+a4=1,a5+a6+a7+a8=2,Sn=15,则项数n为( )
A.12 B.14 C.15 D.16
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-2等差数列及其前n项和(解析版) 题型:解答题
已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对n∈N*,均有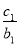 +
+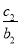 +…+
+…+ =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-1数列的概念与简单表示法(解析版) 题型:解答题
设数列{an}的前n项和为Sn.已知a1=a,an+1=Sn+3n,n∈N*.
(1)设bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N*,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量m=(cos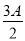 ,sin
,sin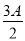 ),n=(cos
),n=(cos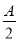 ,sin
,sin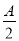 ),且满足|m+n|=
),且满足|m+n|=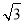 .
.
(1)求角A的大小;
(2)若|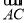 |+|
|+|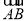 |=
|=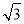 |
|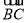 |,试判断△ABC的形状.
|,试判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com