
已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对n∈N*,均有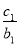 +
+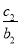 +…+
+…+ =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值.
(1)an=2n-1 bn=3n-1
(2)32014
【解析】【解析】
(1)∵a2=1+d,a5=1+4d,a14=1+13d,
∴(1+4d)2=(1+d)(1+13d),解得d=2(∵d>0).
则an=1+(n-1)×2=2n-1.
又b2=a2=3,b3=a5=9,
∴等比数列{bn}的公比q=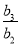 =
=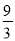 =3.
=3.
∴bn=b2qn-2=3×3n-2=3n-1.
(2)由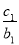 +
+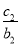 +…+
+…+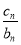 =an+1得
=an+1得
当n≥2时,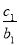 +
+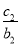 +…+
+…+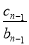 =an,
=an,
两式相减,得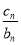 =an+1-an=2,
=an+1-an=2,
∴cn=2bn=2×3n-1(n≥2).
而当n=1时,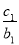 =a2,∴c1=3.
=a2,∴c1=3.
∴cn=
∴c1+c2+c3+…+c2014
=3+2×31+2×32+…+2×32013
=3+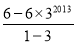
=3-3+32014
=32014.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:解答题
设a≠0,对于函数f(x)=log3(ax2-x+a),
(1)若函数f(x)的定义域为R,求实数a的取值范围;
(2)若函数f(x)的值域为R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:填空题
在数列{an}中,a1=2,an+an+1=1(n∈N*),设Sn为数列{an}的前n项和,则S2007-2S2006+S2005的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:解答题
已知首项为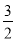 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-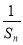 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:选择题
设等比数列{an}的前n项和为Sn,若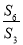 =3,则
=3,则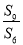 =( )
=( )
A.2 B.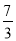 C.
C.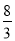 D.3
D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-2等差数列及其前n项和(解析版) 题型:选择题
已知正项数列{an}的前n项和为Sn,且a1=1,an= +
+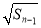 (n≥2),则数列{an}的通项公式为an=( )
(n≥2),则数列{an}的通项公式为an=( )
A.n-1 B.n C.2n-1 D.2n
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-1数列的概念与简单表示法(解析版) 题型:解答题
设数列{an}的前n项和Sn满足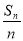 =3n-2.
=3n-2.
(1)求数列{an}的通项公式;
(2)设bn=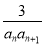 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<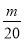 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-4数系的扩充与复数的引入(解析版) 题型:选择题
投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为( )
A.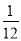 B.
B.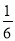 C.
C.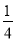 D.
D.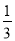
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:选择题
已知点A(1,-2),若向量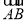 与向量a=(2,3)同向,且|
与向量a=(2,3)同向,且|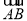 |=
|= ,则点B的坐标为( )
,则点B的坐标为( )
A.(2,3) B.(-2,3) C.(3,1) D.(3,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com