练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设数列{an}的前n项和Sn满足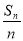＝3n－2.

    (1)求数列{an}的通项公式；

    (2)设bn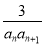＝，Tn是数列{bn}的前n项和，求使得Tn<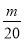对所有n∈N*都成立的最小正整数m.

     

    （1）an＝6n－5(n∈N*)

    （2）10

    【解析】解：(1)由＝3n－2，得Sn＝3n2－2n.

    当n≥2时，an＝Sn－Sn－1＝(3n2－2n)－[3(n－1)2－2(n－1)]＝6n－5；

    当n＝1时，a1＝S1＝3×1－2＝6－5＝1.

    所以an＝6n－5(n∈N*)．

    (2)由(1)得bn＝＝＝ (－)，

    故Tn＝ [(1－)＋(－)＋…＋(－)]＝ (1－)．

    因此，使得(1－)< (n∈N*)成立的m必须满足≤，即m≥10，故满足要求的最小正整数m为10.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-1不等关系与不等式（解析版） 题型：填空题

    已知1≤lg(xy)≤4，－1≤lg≤2，则lg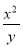的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-4数列求和（解析版） 题型：选择题

    若数列{an}为等比数列，且a1＝1，q＝2，则Tn 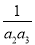＝＋＋…＋的结果可化为(　　)

    A．1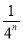－ B．1－

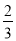    C．(1－) D． (1－)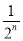

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-2等差数列及其前n项和（解析版） 题型：解答题

    已知等差数列{an}的首项a1＝1，公差d>0，且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项．

    (1)求数列{an}，{bn}的通项公式；

    (2)设数列{cn}对n∈N*，均有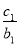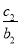＋＋…＋＝an＋1成立，求c1＋c2＋c3＋…＋c2014的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-2等差数列及其前n项和（解析版） 题型：选择题

    在各项均不为零的等差数列{an}中，若－an＋1＝an－1(n≥2，n∈N*)，则S2014的值为(　　)

    A．2013 B．2014 C．4026 D．4028

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-1数列的概念与简单表示法（解析版） 题型：解答题

    设数列{an}的前n项和为Sn.已知a1＝a，an＋1＝Sn＋3n，n∈N*.

    (1)设bn＝Sn－3n，求数列{bn}的通项公式；

    (2)若an＋1≥an，n∈N*，求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-1数列的概念与简单表示法（解析版） 题型：选择题

    已知数列{an}的前n项和为Sn，对任意的n∈N*有S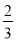n＝an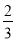－，且1<Sk<12，则k的值为(　　)

    A．2 B．2或4 C．3或4 D．6

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-4数系的扩充与复数的引入（解析版） 题型：选择题

    已知集合M＝{i，i2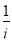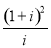，，}，i是虚数单位，Z为整数集，则集合Z∩M中的元素个数是(　　)

    A．3 B．2 C．1 D．0

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-1向量的概念及运算（解析版） 题型：选择题

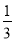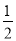
    已知A，B，C是平面上不共线的三点，O是△ABC的重心，动点P满足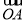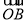＝ (＋＋2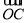)，则点P一定为三角形ABC的(　　)

    A．AB边中线的中点

    B．AB边中线的三等分点(非重心)

    C．重心

    D．AB边的中点

     

    查看答案和解析>>

    同步练习册答案