
在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量m=(cos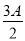 ,sin
,sin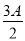 ),n=(cos
),n=(cos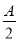 ,sin
,sin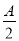 ),且满足|m+n|=
),且满足|m+n|=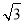 .
.
(1)求角A的大小;
(2)若|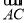 |+|
|+|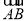 |=
|=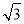 |
|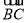 |,试判断△ABC的形状.
|,试判断△ABC的形状.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:解答题
已知首项为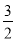 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-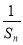 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-4数系的扩充与复数的引入(解析版) 题型:选择题
投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为( )
A.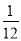 B.
B.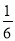 C.
C.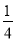 D.
D.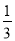
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:解答题
已知向量m=(2cosx, cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+ ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n.
(1)求函数y=f(x)的单调递增区间;
(2)设△ABC的内角A满足f(A)=2,a、b、c分别为角A、B、C所对的边,且 ·
· =
=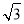 ,求边BC的最小值.
,求边BC的最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:选择题
已知平面向量a,b,|a|=1,|b|=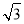 ,且|2a+b|=
,且|2a+b|=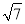 ,则向量a与向量a+b的夹角为( )
,则向量a与向量a+b的夹角为( )
A.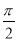 B.
B. C.
C.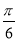 D.π
D.π
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:解答题
已知点O(0,0)、A(1,2)、B(4,5)及 =
= +t
+t ,试问:
,试问:
(1)t为何值时,P在x轴上?在y轴上?P在第三象限?
(2)四边形OABP能否成为平行四边形?若能,求出相应的t值;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:选择题
已知点A(1,-2),若向量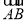 与向量a=(2,3)同向,且|
与向量a=(2,3)同向,且|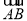 |=
|= ,则点B的坐标为( )
,则点B的坐标为( )
A.(2,3) B.(-2,3) C.(3,1) D.(3,-1)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
对于向量a、b、c和实数λ,下列命题中真命题是( )
A.若a·b=0,则a=0或b=0
B.若λa=0,则λ=0或a=0
C.若a2=b2,则a=b或a=-b
D.若a·b=a·c,则b=c
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:填空题
已知点P(sin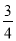 π,cos
π,cos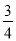 π)落在角θ的终边上,且θ∈[0,2π),则tan(θ+
π)落在角θ的终边上,且θ∈[0,2π),则tan(θ+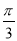 )的值为________.
)的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com