已知平面向量a，b，|a|＝1，|b|＝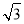
，且|2a＋b|＝
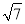，则向量a与向量a＋b的夹角为( )
A．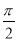
B．
C．
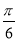D．π
科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-4数列求和（解析版） 题型：选择题
若数列{an}为等比数列，且a1＝1，q＝2，则Tn ＝
＋
＋…＋
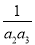的结果可化为( )
A．1－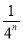
B．1－
C．
(1－
) D．
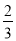(1－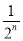
)
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-1数列的概念与简单表示法（解析版） 题型：选择题
已知数列{an}的前n项和为Sn，对任意的n∈N*有S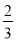n＝
an－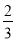
，且1<Sk<12，则k的值为( )
A．2 B．2或4 C．3或4 D．6
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-4数系的扩充与复数的引入（解析版） 题型：选择题
已知集合M＝{i，i2，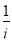
，
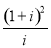}，i是虚数单位，Z为整数集，则集合Z∩M中的元素个数是( )
A．3 B．2 C．1 D．0
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-3平面向量的数量积及应用（解析版） 题型：解答题
设向量a，b满足|a|＝|b|＝1及|3a－2b|＝
．
(1)求a，b夹角的大小；
(2)求|3a＋b|的值．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-2平面向量的基本定理及坐标表示（解析版） 题型：解答题
在△ABC中，角A，B，C所对的边分别为a，b，c，已知向量m＝(cos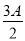
，sin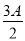
)，n＝(cos
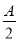，sin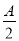
)，且满足|m＋n|＝
.
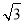(1)求角A的大小；
(2)若|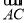
|＋|
|＝
|
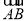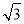|，试判断△ABC的形状．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-2平面向量的基本定理及坐标表示（解析版） 题型：填空题
已知平面直角坐标系xOy上的区域D由不等式组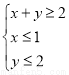
给定，若M(x，y)为D上的动点，A的坐标为(－1,1)，则
·
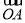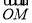的取值范围是________．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-1向量的概念及运算（解析版） 题型：选择题
已知A，B，C是平面上不共线的三点，O是△ABC的重心，动点P满足
＝
(
＋
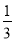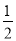
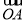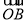＋2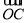
)，则点P一定为三角形ABC的( )
A．AB边中线的中点
B．AB边中线的三等分点(非重心)
C．重心
D．AB边的中点
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-6简单的三角恒等变换（解析版） 题型：解答题
已知函数f(x)＝cos2ωx＋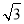
sinωxcosωx－
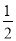(ω>0)的最小正周期为π．
(1)求ω值及f(x)的单调递增区间；
(2)在△ABC中，a，b，c分别是角A，B，C的对边，已知a＝1，b＝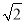
，f(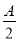
)＝
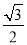，求角C的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＝2，故cos〈a，a＋b〉＝
＝
，所以〈a，a＋b〉＝
．故选B．
