
已知不等式ax2+bx+c>0的解集为(1,t),记函数f(x)=ax2+(a-b)x-c.
(1)求证:函数y=f(x)必有两个不同的零点;
(2)若函数y=f(x)的两个零点分别为m,n,求|m-n|的取值范围;
(3)是否存在这样的实数a,b,c及t使得函数y=f(x)在[-2,1]上的值域为[-6,12]?若存在,求出t的值及函数y=f(x)的解析式;若不存在,请说明理由.
(1)见解析 (2)(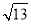 ,+∞) (3)f(x)=-2x2-8x+4.
,+∞) (3)f(x)=-2x2-8x+4.
【解析】【解析】
(1)证明:由题意知a+b+c=0,且-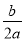 >1,a<0且
>1,a<0且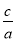 >1,
>1,
∴ac>0,
∴对于函数f(x)=ax2+(a-b)x-c有Δ=(a-b)2+4ac>0,
∴函数y=f(x)必有两个不同零点.
(2)|m-n|2=(m+n)2-4mn=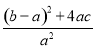 =
=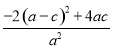 =(
=(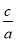 )2+8
)2+8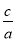 +4,
+4,
由不等式ax2+bx+c>0的解集为(1,t)可知,
方程ax2+bx+c=0的两个解分别为1和t(t>1),
由根与系数的关系知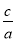 =t,
=t,
∴|m-n|2=t2+8t+4,t∈(1,+∞).
∴|m-n|>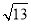 ,∴|m-n|的取值范围为(
,∴|m-n|的取值范围为(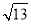 ,+∞).
,+∞).
(3)假设存在满足题意的实数a,b,c及t,
∵f(x)=ax2+(a-b)x-c=a[x2+(1-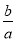 )x-
)x-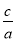 ]
]
=a[x2+(1+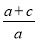 )x-
)x-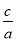 ]
]
=a[x2+(2+t)x-t](t>1),
∴f(x)的对称轴为x=-1-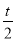 <-
<-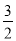 .
.
∴f(x)在[-2,1]上的最小值为f(1)=3a=-6,则a=-2.
要使函数y=f(x)在[-2,1]上的值域为[-6,12],
只要f(x)max=12即可.
①若-1-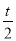 ≤-2,即t≥2,f(x)max=f(-2)=12,则有6t=12,
≤-2,即t≥2,f(x)max=f(-2)=12,则有6t=12,
∴t=2.
此时,a=-2,b=6,c=-4,t=2,∴f(x)=-2x2-8x+4.
②若-1-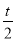 >-2,∴1<t<2,f(x)max=f(-1-
>-2,∴1<t<2,f(x)max=f(-1-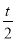 )=
)= =12.
=12.
∴t=2或t=-10,舍去.
综上所述,当a=-2,b=6,c=-4,t=2时,函数y=f(x)在[-2,1]上的值域为[-6,12],此时函数的解析式为f(x)=-2x2-8x+4.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:选择题
若P=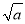 +
+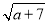 ,Q=
,Q=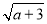 +
+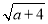 (a≥0),则P,Q的大小关系( )
(a≥0),则P,Q的大小关系( )
A.P>Q B.P=Q
C.P<Q D.由a取值决定
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:解答题
已知lg(3x)+lgy=lg(x+y+1).
(1)求xy的最小值;
(2)求x+y的最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:选择题
已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是( )
A.3 B.4 C.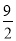 D.
D.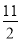
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:解答题
设a≠0,对于函数f(x)=log3(ax2-x+a),
(1)若函数f(x)的定义域为R,求实数a的取值范围;
(2)若函数f(x)的值域为R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:选择题
已知a∈[-1,1],不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为( )
A.(-∞,2)∪(3,+∞) B.(-∞,1)∪(2,+∞)
C.(-∞,1)∪(3,+∞) D.(1,3)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:选择题
已知a<0,-1<b<0,那么下列不等式成立的是( )
A.a>ab>ab2 B.ab2>ab>a
C.ab>a>ab2 D.ab>ab2>a
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:选择题
设等比数列{an}的前n项和为Sn,若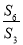 =3,则
=3,则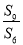 =( )
=( )
A.2 B.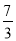 C.
C.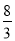 D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com