
某工厂将4名新招聘员工分配至三个不同的车间,每个车间至少分配一名员工,甲、乙
两名员工必须分配至同一车间,则不同的分配方法总数为 (用数字作答).
科目:高中数学 来源:2015届江苏省五校高二下学期期中文科数学试卷(解析版) 题型:填空题
求“方程 的解”有如下解题思路:设
的解”有如下解题思路:设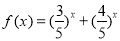 ,则
,则 在
在 上单调递减,且
上单调递减,且 ,所以原方程有唯一解
,所以原方程有唯一解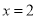 .类比上述解题思路,方程
.类比上述解题思路,方程 的解为 .
的解为 .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省无锡江阴市高二下学期期中考试文科数学试卷(解析版) 题型:填空题
已知 是定义在
是定义在 上的函数,且对任意实数
上的函数,且对任意实数 ,恒有
,恒有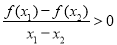 ,且
,且 的最大值为1,则不等式
的最大值为1,则不等式 的解集为 .
的解集为 .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省扬州市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数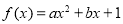 (
( 为实数,
为实数, ),
),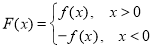 ,⑴若
,⑴若 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
⑵设 ,且函数
,且函数 为偶函数,判断
为偶函数,判断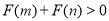 是否大0?
是否大0?
⑶设 ,当
,当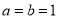 时,证明:对任意实数
时,证明:对任意实数 ,
, (其中
(其中 是
是 的导函数) .
的导函数) .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省扬州市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
设 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足:(i)
满足:(i) ;(ii)对任意
;(ii)对任意 ,当
,当 时,恒有
时,恒有 .那么称这两个集合“保序同构”.现给出以下4对集合. ①
.那么称这两个集合“保序同构”.现给出以下4对集合. ① ;②
;② ;③
;③ ;④
;④ ,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
查看答案和解析>>
科目:高中数学 来源:2015届江苏省扬州市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知 ,命题
,命题 ,命题
,命题 .⑴若命题
.⑴若命题 为真命题,求实数
为真命题,求实数 的取值范围;⑵若命题
的取值范围;⑵若命题 为真命题,命题
为真命题,命题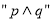 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二第二学期阶段测试理科数学试卷(解析版) 题型:解答题
设函数 的定义域为E,值域为F.
的定义域为E,值域为F.
(1)若E={1,2},判断实数λ=lg22+lg2lg5+lg5﹣ 与集合F的关系;
与集合F的关系;
(2)若E={1,2,a},F={0, },求实数a的值.
},求实数a的值.
(3)若 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二下学期月考数学试卷(解析版) 题型:解答题
已知函数
(1)将 写成
写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(2)如果△ABC的三边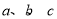 满足
满足 ,且边
,且边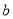 所对的角为
所对的角为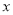 ,试求
,试求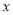 的范围及此时函数
的范围及此时函数 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com