
【题目】某中学有学生500人,学校为了解学生课外阅读时间,从中随机抽取了50名学生,收集了他们2018年10月课外阅读时间(单位:小时)的数据,并将数据进行整理,分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],得到如图所示的频率分布直方图.

(Ⅰ)试估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;
(Ⅱ)已知这50名学生中恰有2名女生的课外阅读时间在[18,20],现从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,求至少抽到1名女生的概率;
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,试估计该校学生2018年10月课外阅读时间的平均数.
【答案】(Ⅰ)150(Ⅱ)![]() (Ⅲ)14.68
(Ⅲ)14.68
【解析】
(Ⅰ)由频率分布直方图求出课外阅读时间不小于16小时的样本的频率为0.30,由此能估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;(Ⅱ)阅读时间在[18,20]的样本的频率为0.10.从而课外阅读时间在[18,20]的样本对应的学生人数为5.这5名学生中有2名女生,3名男生,设女生为A,B,男生为C,D,E,从中抽取2人,利用列举法能求出至少抽到1名女生的概率;(Ⅲ)由频率分布直方图能估计该校学生2018年10月课外阅读时间的平均数.
(Ⅰ)0.10×2+0.05×2=0.30,
即课外阅读时间不小于16小时的样本的频率为0.30.
因为500×0.30=150,
所以估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数为150.
(Ⅱ)阅读时间在[18,20]的样本的频率为0.05×2=0.10.
因为50×0.10=5,即课外阅读时间在[18,20]的样本对应的学生人数为5.
这5名学生中有2名女生,3名男生,设女生为A,B,男生为C,D,E,
从中抽取2人的所有可能结果是:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E).
其中至少抽到1名女生的结果有7个,
所以从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,至少抽到1名女生的概率为p=![]()
(Ⅲ)根据题意,0.08×2×11+0.12×2×13+0.15×2×15+0.10×2×17+0.05×2×19=14.68(小时).
由此估计该校学生2018年10月课外阅读时间的平均数为14.68小时.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,BCD是边长为![]() 的等边三角形,
的等边三角形,![]() ,二面角A﹣BC﹣D的大小为θ,且
,二面角A﹣BC﹣D的大小为θ,且![]() ,则三棱锥A﹣BCD体积的最大值为( )
,则三棱锥A﹣BCD体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】这次新冠肺炎疫情,是新中国成立以来在我国发生的传播速度最快、感染范围最广、防控难度最大的一次重大突发公共卫生事件.中华民族历史上经历过很多磨难,但从来没有被压垮过,而是愈挫愈勇,不断在磨难中成长,从磨难中奋起.在这次疫情中,全国人民展现出既有责任担当之勇、又有科学防控之智.某校高三学生也展开了对这次疫情的研究,一名同学在数据统计中发现,从2020年2月1日至2月7日期间,日期![]() 和全国累计报告确诊病例数量
和全国累计报告确诊病例数量![]() (单位:万人)之间的关系如下表:
(单位:万人)之间的关系如下表:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
全国累计报告确诊病例数量 | 1.4 | 1.7 | 2.0 | 2.4 | 2.8 | 3.1 | 3.5 |
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?
的关系?
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (系数精确到0.01).并预测2月10日全国累计报告确诊病例数.
(系数精确到0.01).并预测2月10日全国累计报告确诊病例数.
参考数据:![]() ,
,![]() ,
, ,
,![]() .
.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
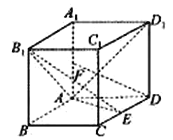
【题目】如图,四棱柱![]() 的底面为菱形,
的底面为菱形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)设![]() 为
为![]() 的中点,根据平几知识可得四边形
的中点,根据平几知识可得四边形![]() 是平行四边形,即得
是平行四边形,即得![]() ,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面
,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面![]() 一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得
一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得![]() 的长.
的长.
试题解析:(1)证明:设![]() 为
为![]() 的中点,连
的中点,连![]()
因为![]()
![]()
![]() ,又
,又![]()
![]()
![]() ,所以
,所以![]()
![]()
![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
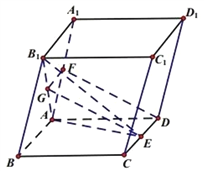
(2)因为![]() 是菱形,且
是菱形,且![]() ,
,
所以![]() 是等边三角形
是等边三角形
取![]() 中点
中点![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
, ![]()
建立如图的空间直角坐标系,令![]() ,
,
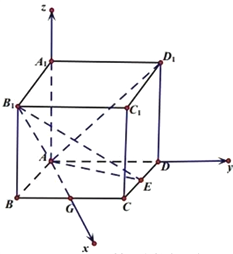
则![]() ,
, 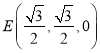 ,
, ![]() ,
, ![]() ,
,
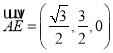 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() 且
且![]() ,
,
取![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则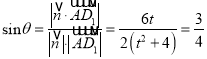 ,
,
解得![]() ,故线段
,故线段![]() 的长为2.
的长为2.
【题型】解答题
【结束】
20
【题目】椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,若椭圆过点
,若椭圆过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
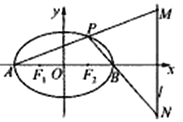
(2)若![]() 为椭圆的左、右顶点,
为椭圆的左、右顶点, ![]() (
(![]() )为椭圆上一动点,设直线
)为椭圆上一动点,设直线![]() 分别交直线
分别交直线![]() :
: ![]() 于点
于点![]() ,判断线段
,判断线段![]() 为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,选项正确的是( )
A. 在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15
的值一定是15
B. 两个变量相关性越强,则相关系数![]() 就越接近于1
就越接近于1
C. 在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关
D. 若某商品的销售量![]() (件)与销售价格
(件)与销售价格![]() (元/件)存在线性回归方程为
(元/件)存在线性回归方程为![]() ,当销售价格为10元时,销售量为100件左右
,当销售价格为10元时,销售量为100件左右
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程与离心率;
的方程与离心率;
(Ⅱ)设椭圆![]() 上不与
上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长是定值.
轴截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 为
为![]() 中点.
中点.
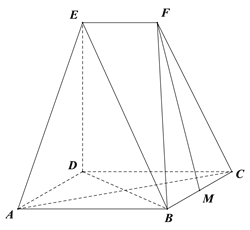
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() 为线段
为线段![]() 上的点,当三棱锥
上的点,当三棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆C的标准方程;
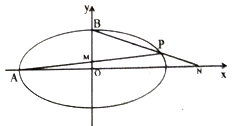
(2)设点P是椭圆C上一点,左顶点为A,上顶点为B,直线PA与y轴交于点M,直线PB与x轴交于点N,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com