
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{9}{8}$ |
分析 由已知得-$\frac{1}{2}$≤sinx≤1,利用同角平方关系对函数f(x)化简,结合二次函数的性质求出函数的最大、最小值.
解答 解:由正弦函数的性质可知,
当x∈[$\frac{π}{6}$,$\frac{7π}{6}$]时,sinx∈[-$\frac{1}{2}$,1];
∵函数f(x)=3-sinx-2cos2x
=2sin2x-sinx+1
=2${(sinx-\frac{1}{4})}^{2}$+$\frac{7}{8}$;
∴当sinx=$\frac{1}{4}$时,f(x)取得最小值为f(x)min=$\frac{7}{8}$;
当sinx=1或-$\frac{1}{2}$时,f(x)取得最大值为f(x)max=2;
∴函数的最大值与最小值之差为f(x)max-f(x)min=2-$\frac{7}{8}$=$\frac{9}{8}$.
故选:D.
点评 本题考查了正弦函数的性质以及利用配方法求二次函数的值域问题,要注意sinx的范围.


科目:高中数学 来源: 题型:选择题
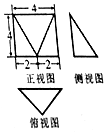
| A. | 36π | B. | $\frac{64\sqrt{2}}{3}$π | C. | 8$\sqrt{6}$π | D. | $\frac{8}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=2 n=2 | B. | m=2 n=6 | C. | m=3 n=7 | D. | m=3 n=8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=-{x^{\frac{1}{2}}}$ | B. | y=-x2+|x| | C. | y=ln|x| | D. | y=-x2+x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com