
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
分析 由题意,z=400x+300y,约束条件$\left\{\begin{array}{l}{3x+2y≤20}\\{3x+y≤20}\\{2x+5y≤25}\\{x≥0,y≥0}\end{array}\right.$,求得最优解,即求得利润的最大值和最大值的状态.
解答  解:由题意,z=400x+300y,约束条件$\left\{\begin{array}{l}{3x+2y≤20}\\{3x+y≤20}\\{2x+5y≤25}\\{x≥0,y≥0}\end{array}\right.$,如图所示,
解:由题意,z=400x+300y,约束条件$\left\{\begin{array}{l}{3x+2y≤20}\\{3x+y≤20}\\{2x+5y≤25}\\{x≥0,y≥0}\end{array}\right.$,如图所示,
作直线4x+3y=0,并移动,可知当移动后的直线过B($\frac{50}{11}$,$\frac{35}{11}$)时,4x+3y取得最大值,
则z=400x+300y取得最大值,故zmax=$\frac{30500}{11}$,
∴生产“沉鱼落雁”$\frac{50}{11}$吨,“国色天香”$\frac{35}{11}$吨,才可以获得最大周利润$\frac{30500}{11}$元.
点评 本题主要考查用简单的线性规划研究目标函数的最大和最小值,关键是通过平面区域,求得最优解,属于线性规划的应用题.


科目:高中数学 来源: 题型:解答题
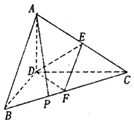 已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.
已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n | B. | 2n-1 | C. | 2n-1 | D. | 2n-1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
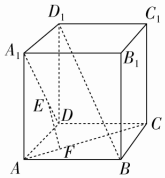 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )| A. | EF至多与A1D、AC之一垂直 | B. | EF与A1D、AC都垂直 | ||
| C. | EF与BD1相交 | D. | EF与BD1异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{9}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com