
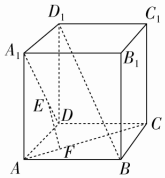
 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )| A. | EF至多与A1D、AC之一垂直 | B. | EF与A1D、AC都垂直 | ||
| C. | EF与BD1相交 | D. | EF与BD1异面 |
分析 连接D1E,BF,根据A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,判断D1E,BF交与同一点M,再根据成比例线段证明EF∥D1B,由D1B⊥AC,D1B⊥A1D证明EF与A1D、AC都垂直.
解答 解:如图所示;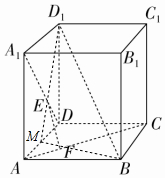
连接D1E,与AD交与M点处,因为A1E=$\frac{2}{3}$A1D,所以DM=$\frac{1}{2}$A1D1=$\frac{1}{2}$AD,
所以M为AD中点,
连接BF,交AD与N点,因为AF=$\frac{1}{3}$AC,所以AN=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
所以N为AD中点,
所以M,N重合;且$\frac{ME}{{ED}_{1}}$=$\frac{MF}{FB}$=$\frac{1}{2}$,所以EF∥D1B,
又AC⊥平面DD1B,所以AC⊥BD1,
所以AC⊥EF,
同理,A1D⊥EF,
所以EF与A1D、AC都垂直,且相交,
∴B正确,A、EF至多与A1D、AC之一垂直错误,
C、EF与BD1相交错误,D、EF与BD1异面错误.
故选:B.
点评 本题考查了立体几何中线线平行与垂直的判断问题,是综合性问题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
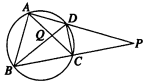 如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )
如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )| A. | 4对 | B. | 2对 | C. | 5对 | D. | 3对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com