
分析 (Ⅰ)由于x=3是f(x)的极值点,则f′(3)=0求出a,进而求出f′(x)>0得到函数的增区间,求出f′(x)<0得到函数的减区间即可;
(Ⅱ)由于f(x)≥1恒成立,即x>0时,$\frac{1}{2}$x2-(a+1)x+alnx≥0恒成立,设g(x)=$\frac{1}{2}$x2-(a+1)x+alnx,求出函数的导数,分类讨论参数a,得到函数g(x)的最小值≥0,即可得到a的范围.
解答 解:(Ⅰ)f′(x)=x-(a+1)+$\frac{a}{x}$,
∵x=3是f(x)的极值点,
∴f′(3)=3-(a+1)+$\frac{a}{3}$=0,解得a=3,
当a=3时,f′(x)=$\frac{(x-1)(x-3)}{x}$,
当x变化时,
| x | (0,1) | 1 | (1,3) | 3 | (3,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
点评 本题考查利用导数研究函数的单调性及函数恒成立时所取的条件.考查考生的运算、推导、判断能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{16}$+$\frac{{x}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
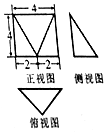
| A. | 36π | B. | $\frac{64\sqrt{2}}{3}$π | C. | 8$\sqrt{6}$π | D. | $\frac{8}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com