
分析 (1)求出函数的导数,计算f′(1),f(1)的值,求出切线方程即可;
(2)解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
解答 解:(1)由f(x)=$\frac{1}{3}$x3-x2-3x-$\frac{1}{3}$,
知f′(x)=x2-2x-3,
∴f′(1)=-4,所以函数在x=1处的切线的斜率为-4,
又∵f(1)=-4,
故切线方程为y+4=-4(x-1),即y=-4x;
(2)令f′(x)=0,得x=-1或x=3,
x变化时,f′(x),f(x)的变化情况如下:
| x | (-∞,-1) | -1 | (-1,3) | 3 | (3,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
点评 本题考查了函数的单调性、极值问题,考查切线方程,是一道中档题.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
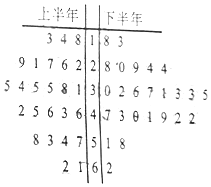 自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com