Question

【题目】如图，△ABC中，∠BAC＝90°，∠ABC＝30°．△ABD中，∠ADB＝90°，∠ABD＝45°，且AC＝1．将△ABD沿边AB折叠后，

（1）若二面角C—AB—D为直二面角，则直线CD与平面ABC所成角的正切值为_______；

（2）若二面角C—AB—D的大小为150°，则线段CD的长为_______．

Answer 1

【答案】

【解析】

作出二面角的平面角.

（1）当二面角为直角时，判断出直线与平面所成的角，解直角三角形求得线面角的正切值.

（2）当二面角大小为时，结合余弦定理进行解三角形，由此求得的长.

依题意ABC中，∠BAC＝90°，∠ABC＝30°．△ABD中，∠ADB＝90°，∠ABD＝45°，且AC＝1．所以，.设分别是的中点，所以,，所以是二面角的平面角，.

（1）当二面角为直角时，由于，根据面面垂直的性质定理可知平面，所以是直线img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/17/39a1a048/SYS202011261741258328971401_DA/SYS202011261741258328971401_DA.004.png" width="29" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />与平面所成的角.在中.

（2）当二面角大小为时，即，在三角形中，由余弦定理得.在三角形和三角形中，，由余弦定理得，，.

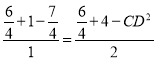故答案为：(1). (2).