
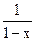 的一个零点.若
的一个零点.若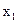 ∈(1,
∈(1,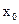 ),
),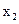 ∈(
∈(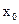 ,+
,+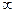 ),则
),则A.f(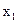 )<0,f( )<0,f(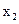 )<0 )<0 | B.f(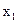 )<0,f( )<0,f(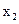 )>0 )>0 |
C.f(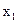 )>0,f( )>0,f(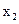 )<0 )<0 | D.f(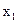 )>0,f( )>0,f(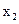 )>0 )>0 |
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
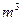 ,深为5
,深为5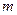 的长方体无盖蓄水池,池壁的造价为95
的长方体无盖蓄水池,池壁的造价为95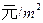 ,池底的造价为135
,池底的造价为135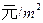 ,若水池底的一边长为
,若水池底的一边长为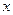
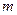 ,水池的总造价为
,水池的总造价为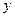 元。(1)把水池总造价
元。(1)把水池总造价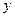
 表示为
表示为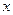 的函数。(2)当水池
的函数。(2)当水池 的长
的长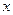 为多少时,水池的总造价最少?
为多少时,水池的总造价最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
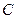 ,公路
,公路 恰好是
恰好是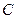 的准线,
的准线,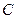 上的点
上的点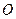 到
到 的距离最近,且为
的距离最近,且为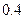 千米,城镇
千米,城镇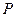 位于点
位于点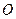 的北偏东
的北偏东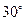 处,
处,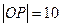 千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路
千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路 以便建立水陆交通网.
以便建立水陆交通网.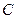 的方程;
的方程;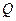 的位置),并求公路总长的最小值(精确到0.001千米)
的位置),并求公路总长的最小值(精确到0.001千米)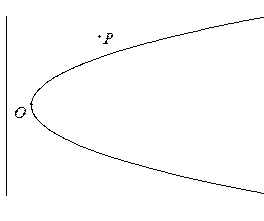
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
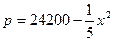 ,
,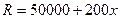 (元)。
(元)。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
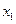 ,
,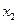 ,……
,……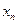 中的最大数为max
中的最大数为max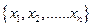 ,最小数为min
,最小数为min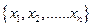 。已知ABC的三边长位a,b,c(
。已知ABC的三边长位a,b,c(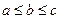 ),定义它的亲倾斜度为
),定义它的亲倾斜度为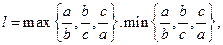
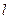 =1”是“
=1”是“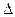 ABC为等边三角形”的
ABC为等边三角形”的| A.必要而不充分的条件 |
| B.充分而不必要的条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com