
分析 由题意设出球的半径,圆M的半径,二者与OM构成直角三角形,求出圆M的半径,然后可求球的表面积,圆锥的表面积,再求二者之比.
解答 解:设球的半径为R,圆M的半径r,
则R2=$\frac{1}{4}$R2+r2,
∴$\frac{3}{4}$R2=r2,∴S球=4πR2,
圆锥的表面积为:πr2+πr$\sqrt{\frac{9}{4}{R}^{2}+{r}^{2}}$=$\frac{9}{4}$πR2,
则所得圆锥的表面积与球的表面积的比为$\frac{9}{16}$,
故答案为$\frac{9}{16}$.
点评 本题是基础题,考查球的体积、表面积的计算,仔细体会,理解并能够应用小圆的半径、球的半径、以及球心与圆心的连线的关系,是本题的突破口.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
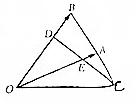 在△ABO中,点C是点B关于点A的对称点,点D是OB靠近B的三等分点,DC与OA交于E点,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OC}$,$\overrightarrow{CD}$.
在△ABO中,点C是点B关于点A的对称点,点D是OB靠近B的三等分点,DC与OA交于E点,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OC}$,$\overrightarrow{CD}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1为正方形ABCD的边长为2,AC∩BD=O,将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD(如图2)
如图1为正方形ABCD的边长为2,AC∩BD=O,将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD(如图2)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{14}{3}$ | C. | $\frac{26}{3}$ | D. | $\frac{38}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com