Question

20．已知偶函数y=f（x）是定义域为R，当x≥0时，f（x）=$\left\{\begin{array}{l}{3sin\frac{π}{2}x，0≤x≤1}\\{{2}^{2-x}+1，x＞1}\end{array}\right.$．函数g（x）=x²-2ax+a²-1（a∈R），若函数y=g[f（x）]有且仅有6个零点，则实数a的取值范围为（1，2）．

Answer 1

分析 由g（x）=x²-2ax+a²-1=（x-a-1）（x-a+1）可知g[f（x）]=0可化为f（x）=a+1或f（x）=a-1；作函数f（x）的图象，从而可得$\left\{\begin{array}{l}{0＜a-1≤1}\\{1＜a+1＜3}\end{array}\right.$或$\left\{\begin{array}{l}{1＜a-1＜3}\\{a+1=3}\end{array}\right.$；从而解得．

解答 解：∵g（x）=x²-2ax+a²-1=（x-a-1）（x-a+1），
∴g[f（x）]=0可化为f（x）=a+1或f（x）=a-1；
作函数f（x）的图象如下，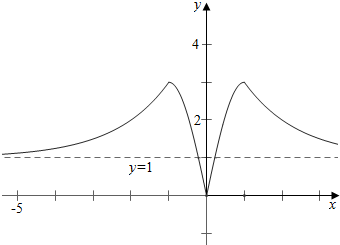
，
结合图象可知，$\left\{\begin{array}{l}{0＜a-1≤1}\\{1＜a+1＜3}\end{array}\right.$或$\left\{\begin{array}{l}{1＜a-1＜3}\\{a+1=3}\end{array}\right.$；
即1＜a＜2，
故答案为：（1，2）．

点评 本题考查了复合函数的应用及数形结合的思想应用．