Question

13．已知函数f（x）=|x²-2ax+b|（x∈R），给出下列命题：
①若a²-b≤0，则f（x）在区间[a，+∞）上是增函数；
②?a∈R，使f（x）为偶函数；
③若f（0）=f（2），则f（x）的图象关于x=1对称；
④若a²-b-2＞0，则函数h（x）=f（x）-2有2个零点．
其中正确命题的序号为①②．

Answer 1

分析 ①由条件可得f（x）=|（x-a）²+b-a²|=（x-a）²+b-a²在区间[a，+∞）上是增函数，即可判断；
②当a=0时，f（x）=|x²+b|显然是偶函数，即可判断；
③由f（0）=f（2），则|b|=|4-4a+b|，取a=0，b=-2，此式成立，此时函数化为f（x）=|x²-2|，其图象不关于x=1对称，即可判断；
④画出图象可知，h（x）=|（x-a）²+b-a²|-2有4个零点，即可判断．

解答 解：①若a²-b≤0，则f（x）=|（x-a）²+b-a²|=（x-a）²+b-a²在区间[a，+∞）上是增函数，
故①正确；
②当a=0时，f（x）=|x²+b|显然是偶函数，故②正确；
③取a=0，b=-2，函数f（x）=|x²-2ax+b|化为f（x）=|x²-2|，满足f（0）=f（2），
但f（x）的图象不关于x=1对称，故③错误；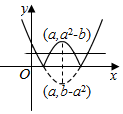
④a²-b-2＞0，即为b-a²＜-2，即a²-b＞2，
则h（x）=|（x-a）²+b-a²|-2有4个零点，故④错误．
∴正确命题为①②．
故答案为：①②．

点评 本题考查了命题的真假判断与应用，考查了二次函数的性质，注意运用数形结合的思想方法，考查判断能力和推理能力，是中档题．