
分析 由题意,方程f(x)=ax恰有两个不同实数根,等价于y=f(x)与y=ax有2个交点,又a表示直线y=ax的斜率,作出图象从而求出a的取值范围.
解答 解:∵方程f(x)=ax恰有两个不同实根,
∴y=f(x)与y=ax有2个交点,a表示直线y=ax的斜率,
作函数f(x)的图象如右图,
当x>1时,当y=ax与f(x)=lnx,相切时,只有一个交点,
此时f′(x)=$\frac{1}{x}$,设切点为(x0,y0),k=$\frac{1}{x_0}$,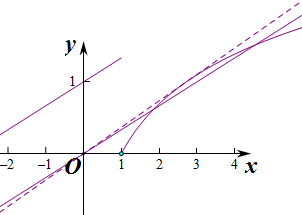
∴切线方程为y-y0=$\frac{1}{x_0}$(x-x0),而切线过原点,
∴y0=1,x0=e,k=$\frac{1}{e}$,
∴直线y=ax的斜率为k=$\frac{1}{e}$,
又∵直线l2与y=$\frac{1}{3}$x+1平行,f(x)与y=ax有两个交点,满足条件.
∴实数a的取值范围是[$\frac{1}{3}$,$\frac{1}{e}$),
故答案为:[$\frac{1}{3}$,$\frac{1}{e}$)
点评 本题考查函数与方程的应用,利用条件转化为两个函数的交点个数问题,利用数形结合是解决本题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:解答题
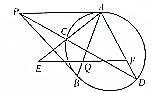 如图,过圆外一点P作圆的两条切线PA、PB,A,B为切点,再过P点作圆的一条割线分别与圆交于点C、D,过AB上任一点Q作PA的平行线分别与直线AC、AD交于点E,F,证明:QE=QF.
如图,过圆外一点P作圆的两条切线PA、PB,A,B为切点,再过P点作圆的一条割线分别与圆交于点C、D,过AB上任一点Q作PA的平行线分别与直线AC、AD交于点E,F,证明:QE=QF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 己知:如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD⊥底面ABCD,PA=PD.
己知:如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD⊥底面ABCD,PA=PD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
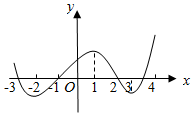 如图y=f(x)的导函数的图象,现有四种说法:
如图y=f(x)的导函数的图象,现有四种说法:| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com