
已知函数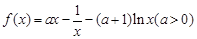 .
.
(1)若曲线 在点
在点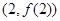 处的切线与直线
处的切线与直线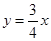 平行,求实数
平行,求实数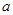 的值;
的值;
(2)若函数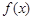 在
在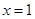 处取得极小值,且
处取得极小值,且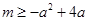 ,求实数
,求实数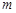 的取值范围.
的取值范围.
(1)2;(2)
解析试题分析:(1)利用函数在某点的导数就是该点的切线切线斜率将切线的斜率用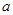 表示出来,再根据两直线平行斜率相等及已知,列出关于
表示出来,再根据两直线平行斜率相等及已知,列出关于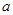 的方程,解出参数
的方程,解出参数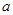 的值;(2)求出函数
的值;(2)求出函数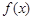 导数
导数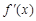 ,利用导数求函数的极值方法,通过分类讨论求出
,利用导数求函数的极值方法,通过分类讨论求出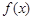 的极值,结合函数
的极值,结合函数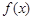 在
在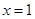 处取得极小值这一条件确定参数
处取得极小值这一条件确定参数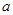 的取值范围,再求出
的取值范围,再求出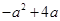 在此范围下的最大值,利用由
在此范围下的最大值,利用由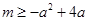 恒成立知
恒成立知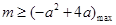 ,求出实数
,求出实数 的取值范围.
的取值范围.
试题解析:(1)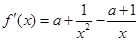 ,由
,由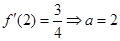
(2)由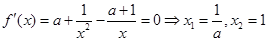
①当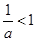 ,即
,即 时,函数
时,函数 在
在 上单调递增,在
上单调递增,在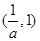 上单调递减,在
上单调递减,在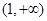 上单调递增
上单调递增
即函数 在
在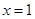 处取得极小值
处取得极小值
②当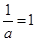 ,即
,即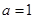 时,函数
时,函数 在
在 上单调递增,无极小值,所以
上单调递增,无极小值,所以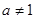
③当 ,即
,即 时,函数
时,函数 在
在 上单调递增,在
上单调递增,在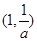 上单调递减,在
上单调递减,在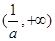 上单调递增
上单调递增
即函数 在
在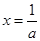 处取得极小值,与题意不符合
处取得极小值,与题意不符合
即 时,函数
时,函数 在
在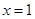 处取得极小值,又因为
处取得极小值,又因为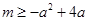 ,所以
,所以 .
.
考点:1.导数的集合意义;2.利用导数求函数的极值;3.分类整合思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;
(2)求函数 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线 与曲线
与曲线 没有公共点,求
没有公共点,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形 (如图所示,其中O为圆心,
(如图所示,其中O为圆心,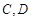 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).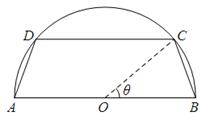
(1)求V关于θ的函数表达式;
(2)求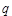 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数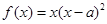 ,
,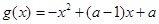 (其中
(其中 为常数).
为常数).
(1)如果函数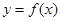 和
和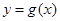 有相同的极值点,求
有相同的极值点,求 的值;
的值;
(2)设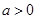 ,问是否存在
,问是否存在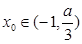 ,使得
,使得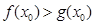 ,若存在,请求出实数
,若存在,请求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(3)记函数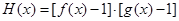 ,若函数
,若函数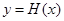 有5个不同的零点,求实数
有5个不同的零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经销商用一辆 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算, 型卡车满载行驶时,每100km所消耗的燃油量
型卡车满载行驶时,每100km所消耗的燃油量 (单位:
(单位: )与速度
)与速度 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
(1)设运送这车水果的费用为 (元)(不计返程费用),将
(元)(不计返程费用),将 表示成速度
表示成速度 的函数关系式;
的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
(1)求曲线y=f(x)在(2,f(2))处的切线方程;
(2)若g(x)=f(x)一 有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
(3)设q>p>2,求证:当x∈(p,q)时, .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com