
分析 (1)设Q(x,y),P(x′,y′),由$\overrightarrow{OQ}$=2$\overrightarrow{PO}$,可得(x,y)=-2(x′,y′),可得$\left\{\begin{array}{l}{{x}^{′}=-\frac{1}{2}x}\\{{y}^{′}=-\frac{1}{2}y}\end{array}\right.$,代入曲线C1的方程可得曲线C2的方程.
(2)设P(2cosθ,sinθ),则Q(-4cosθ,-2sinθ).利用数量积运算性质可得:$\overrightarrow{{F_1}P}•\overrightarrow{{F_2}Q}$=-6$(cosθ+\frac{\sqrt{3}}{2})^{2}$-$\frac{1}{2}$,利用二次函数与三角函数的值域即可得出.
(3)设P(2cosθ,sinθ),则Q(-4cosθ,-2sinθ).设经过点P的直线方程为:y-sinθ=k(x-2cosθ),M(x1,y1),N(x2,y2).与椭圆方程联立化为:(1+4k2)x2-8k(sinθ-2kcosθ)x+4(sinθ-2kcosθ)2-16=0,可得|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$,点Q到直线l的距离d.可得S△QMN=$\frac{1}{2}$d|MN|,通过三角函数代换,利用二次函数的单调性即可得出.
解答 解:(1)设Q(x,y),P(x′,y′),∵$\overrightarrow{OQ}$=2$\overrightarrow{PO}$,∴(x,y)=-2(x′,y′),可得$\left\{\begin{array}{l}{{x}^{′}=-\frac{1}{2}x}\\{{y}^{′}=-\frac{1}{2}y}\end{array}\right.$,代入$\frac{({x}^{′})^{2}}{4}$+(y′)2=1,可得$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1,
∴曲线C2的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1.
(2)F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0).设P(2cosθ,sinθ),则Q(-4cosθ,-2sinθ).
则$\overrightarrow{{F_1}P}•\overrightarrow{{F_2}Q}$=(2cosθ+$\sqrt{3}$,sinθ)•(-4cosθ-$\sqrt{3}$,-2sinθ)=(2cosθ+$\sqrt{3}$)(-4cosθ-$\sqrt{3}$)+sinθ(-2sinθ)=-6$(cosθ+\frac{\sqrt{3}}{2})^{2}$-$\frac{1}{2}$,
∵cosθ∈[-1,1],∴$\overrightarrow{{F_1}P}•\overrightarrow{{F_2}Q}$∈$[-11-6\sqrt{3},-\frac{1}{2}]$.
(3)设P(2cosθ,sinθ),则Q(-4cosθ,-2sinθ).
设经过点P的直线方程为:y-sinθ=k(x-2cosθ),M(x1,y1),N(x2,y2).
联立$\left\{\begin{array}{l}{y-sinθ=k(x-2cosθ)}\\{{x}^{2}+4{y}^{2}=16}\end{array}\right.$,化为:(1+4k2)x2-8k(sinθ-2kcosθ)x+4(sinθ-2kcosθ)2-16=0,
∴x1+x2=$\frac{8k(sinθ-2kcosθ)}{1+4{k}^{2}}$,x1x2=$\frac{4(sinθ-2kcosθ)^{2}-16}{1+4{k}^{2}}$,
∴|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\frac{4\sqrt{1+{k}^{2}}\sqrt{4+16{k}^{2}-(sinθ-2kcosθ)^{2}}}{1+4{k}^{2}}$,
点Q到直线l的距离d=$\frac{|-4kcosθ+2sinθ+sinθ-2kcosθ|}{\sqrt{1+{k}^{2}}}$=$\frac{3|sinθ-2kcosθ|}{\sqrt{1+{k}^{2}}}$.
∴S△QMN=$\frac{1}{2}$d|MN|=6|sinθ-2kcosθ|$\sqrt{4+16{k}^{2}-(sinθ-2kcosθ)^{2}}$.
令|sinθ-2kcosθ|=$\sqrt{1+4{k}^{2}}$|sinα|,
则S△QMN=6|sinα|$\sqrt{4-si{n}^{2}α}$,令|sinα|=t∈[-1,1],
∴S△QMN=6t$\sqrt{4-{t}^{2}}$=f(t),令|sinα|=t∈[-1,1],
则f2(t)=-36t4+144t2=-36(t2-2)2+144,
当且仅当t2=1时,f(t)取得最大值6$\sqrt{3}$.
点评 本题考查了椭圆的标准方程及其参数方程、三角函数的值域、二次函数的单调性、直线与椭圆相交弦长公式、三角形面积计算公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
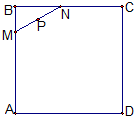 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )| A. | $\frac{7}{8}$ | B. | $\frac{π}{16}$ | C. | $1-\frac{π}{16}$ | D. | $\frac{3}{4}+\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α<β | B. | cosα<cosβ | C. | tanα<tanβ | D. | sinα>sinβ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{9}{4}$ | B. | -$\frac{4}{9}$ | C. | -$\frac{3}{8}$ | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com