
 ��֪������ABCD-A1B1C1D1����E��F��G�ֱ����߶�B1B��AB��A1C�ϵĶ��㣬�۲�ֱ��CE��D1F��CE��D1G���������н��ۣ�
��֪������ABCD-A1B1C1D1����E��F��G�ֱ����߶�B1B��AB��A1C�ϵĶ��㣬�۲�ֱ��CE��D1F��CE��D1G���������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� ����ֱ����ֱ�ߡ�ֱ����ƽ���λ�ù�ϵ���ֱ����ѡ������ų����ܵó����ۣ�
��� �⣺��ֻ��D1F��ƽ��BCC1B1����D1F��ƽ��ADD1A1ʱ��
�������������������ĵ�E�����ڵ�F��ʹ��D1F��CE��
�߹�D1����ƽ��DD1A1A��ֱ��ֱ��ֻ��һ��D1C1��
��D1C1��AB��
��ٴ���
�ڵ���E��B1�غ�ʱ��
CE��AB����CE$��A{D}_{{1}_{\;}}$��
��CE��ƽ��ABD1��
�߶�����������ĵ�F������D1F?ƽ��ABD1��
�������������ĵ�F�����ڵ�E��ʹ��CE��D1F��
�����ȷ��
��ֻ��CE��ֱD1G��ƽ��BCC1B1�е���Ӱʱ��D1G��CE��
�����ȷ��
��ֻ��CE��ƽ��A1CD1ʱ���ܲ���ȷ��
�߹�C���ƽ��A1CD1�Ĵ�����BB1���㣬
��ܴ���
��ѡC��
���� ���⿼��ֱ����ֱ�ߡ�ֱ����ƽ���λ�ù�ϵ���жϣ����е��⣬����ʱҪע��ռ�˼ά������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
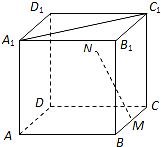 ��ͼ������������ABCD-A1B1C1D1��MΪBC���е㣬��N���ı���CDD1C1�����ڲ��˶�����MN��A1C1����N��Ĺ켣Ϊ��������
��ͼ������������ABCD-A1B1C1D1��MΪBC���е㣬��N���ı���CDD1C1�����ڲ��˶�����MN��A1C1����N��Ĺ켣Ϊ��������| A�� | �߶� | B�� | Բ��һ���� | C�� | ��Բ��һ���� | D�� | ˫���ߵ�һ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2670 | B�� | 2671 | C�� | 2672 | D�� | 2673 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com