
 如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.若△ABD的面积为7,则AB=$\sqrt{37}$.
如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.若△ABD的面积为7,则AB=$\sqrt{37}$. 分析 由已知利用同角三角函数基本关系式可求sin∠ADB,利用两角差的正弦函数公式可求sin∠C的值,从而在△ADC中,由正弦定理可求AD的值,进而利用三角形面积公式可求BD,在△ADB中,利用余弦定理即可求得AB的值.
解答 解:因为$cos∠ADB=-\frac{{\sqrt{2}}}{10}$,
所以$sin∠ADB=\frac{{7\sqrt{2}}}{10}$.
又因为$∠CAD=\frac{π}{4}$,
所以$∠C=∠ADB-\frac{π}{4}$,
所以$sin∠C=sin(∠ADB-\frac{π}{4})=sin∠ADBcos\frac{π}{4}-cos∠ADBsin\frac{π}{4}$=$\frac{{7\sqrt{2}}}{10}•\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{10}•\frac{{\sqrt{2}}}{2}=\frac{4}{5}$.
在△ADC中,由正弦定理得$\frac{AD}{sin∠C}=\frac{AC}{sin∠ADC}$,
故$AD=\frac{AC•sin∠C}{sin∠ADC}=\frac{AC•sin∠C}{sin(π-∠ADB)}=\frac{AC•sin∠C}{sin∠ADB}=\frac{{\frac{7}{2}×\frac{4}{5}}}{{\frac{{7\sqrt{2}}}{10}}}=2\sqrt{2}$.
又${S_{△ABD}}=\frac{1}{2}•AD•AB•sin∠ADB=\frac{1}{2}•2\sqrt{2}•BD•\frac{{7\sqrt{2}}}{10}=7$,解得BD=5.
在△ADB中,由余弦定理得:$A{B^2}=A{D^2}+B{D^2}-2AD•BD•cos∠ADB=8+25-2×2\sqrt{2}×5×(-\frac{{\sqrt{2}}}{10})={37}$.
可得:AB=$\sqrt{37}$.
故答案为:$\sqrt{37}$.
点评 本题主要考查了同角三角函数基本关系式,两角差的正弦函数公式,正弦定理,三角形面积公式,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 80 | |
| 女学生 | |||
| 总计 | 70 | 30 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
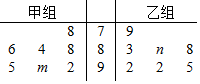 某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )
某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com