
分析 首先分析题目求在面积为S的△ABC的边AB上任取一点P,使S△PBC≤$\frac{1}{3}$S△ABC得到三角形高的关系,利用几何概型求概率.
解答 解:设P到BC的距离为h,
∵三角形ABC的面积为S,设BC边上的高为d,
因为两个三角形有共同的边BC,所以满足S△PBC≤$\frac{1}{3}$S△ABC 时,h≤$\frac{1}{3}$d,所以使S△PBC≤$\frac{1}{3}$S△ABC的概率为$\frac{{S}_{△PBC}}{{S}_{△ABC}}=\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 本题考查了几何概型的概率计算,利用测度(长度、面积、体积)比求几何概型概率.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{e}$,-$\frac{4}{{e}^{2}}$] | B. | [-$\frac{2}{e}$,2e] | C. | [-$\frac{4}{{e}^{2}}$,2e] | D. | [$\frac{4}{{e}^{2}}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.若△ABD的面积为7,则AB=$\sqrt{37}$.
如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.若△ABD的面积为7,则AB=$\sqrt{37}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
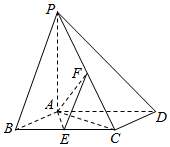 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | -1 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com