
| A. | [-$\frac{2}{e}$,-$\frac{4}{{e}^{2}}$] | B. | [-$\frac{2}{e}$,2e] | C. | [-$\frac{4}{{e}^{2}}$,2e] | D. | [$\frac{4}{{e}^{2}}$,+∞) |
分析 设M(x,kx),则N(x,2e-kx),推导出k=-$\frac{2}{x}lnx$,由此利用导数性质能求出实数k的取值范围.
解答 解:∵函数f(x)=kx,g(x)=2lnx+2e($\frac{1}{e}$≤x≤e2),
f(x)与g(x)的图象上分别存在点M,N,使得M,N关于直线y=e对称,
∴设M(x,kx),则N(x,2e-kx),
∴2e-kx=2lnx+2e,∴k=-$\frac{2}{x}lnx$,
${k}^{'}=\frac{-2+2lnx}{{x}^{2}}$,由k′=0,得x=e,
∵$\frac{1}{e}$≤x≤e2,∴x∈[$\frac{1}{e}$,e)时,k′<0,k=-$\frac{2}{x}lnx$是减函数;
x∈(e,e2]时,k′>0,$k=-\frac{2}{x}lnx$是增函数,
∴x=e时,k=-$\frac{2}{e}lne=-\frac{2}{e}$;x=e2时,k=-$\frac{2}{{e}^{2}}ln{e}^{2}$=-$\frac{4}{{e}^{2}}$;x=$\frac{1}{e}$时,k=-$\frac{2}{\frac{1}{e}}ln(\frac{1}{e})=2e$,
∴kmin=-$\frac{2}{e}lne=-\frac{2}{e}$,kmax=-$\frac{2}{\frac{1}{e}}ln(\frac{1}{e})$=2e.
∴实数k的取值范围是[-$\frac{2}{e}$,2e].
故选:B.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,l∥β,则 α∥β | B. | 若l∥α,l⊥β,则α⊥β | ||
| C. | 若α⊥β,l⊥α,则 l⊥β | D. | 若α⊥β,l∥α,则l⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
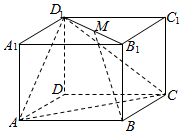 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 80 | |
| 女学生 | |||
| 总计 | 70 | 30 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com