
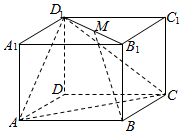
 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.分析 (1)连接BD,与AC相交于O,连接OD1,则O是BD的中点,证明D1MBO是平行四边形,可得D1O∥MB,即可证明BM∥平面D1AC
(2)利用三棱锥的体积公式求B1到平面D1AC的距离.
解答 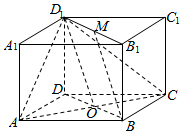 (1)证明:连接BD,与AC相交于O,连接OD1,则O是BD的中点,
(1)证明:连接BD,与AC相交于O,连接OD1,则O是BD的中点,
∵M是线段B1D1的中点,
∴D1M∥BO,D1M=BO,
∴D1MBO是平行四边形,
∴D1O∥MB,
∵BM?平面D1AC,D1O?平面D1AC
∴BM∥平面D1AC;
(2)解:∵AB=4,AD=AA1=3,
∴${V}_{{B}_{1}-{D}_{1}AC}$=4×3×3-$\frac{1}{3}×4×3×3$×$\frac{1}{2}$×3=18,
∵△D1AC中,D1A=3$\sqrt{2}$,D1C=5=AC,
∴${S}_{△{D}_{1}AC}$=$\frac{1}{2}×3\sqrt{2}×\sqrt{25-(\frac{3\sqrt{2}}{2})^{2}}$=$\frac{3\sqrt{41}}{2}$,
设B1到平面D1AC的距离为h,则$\frac{1}{3}×\frac{3\sqrt{41}}{2}h$=18,∴h=$\frac{36\sqrt{41}}{41}$.
点评 本题考查了线面平行的判定定理,考查点面的距离以及数形结合思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{13}}}{3}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,1] | C. | (-∞,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{e}$,-$\frac{4}{{e}^{2}}$] | B. | [-$\frac{2}{e}$,2e] | C. | [-$\frac{4}{{e}^{2}}$,2e] | D. | [$\frac{4}{{e}^{2}}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 60 | ||
| 捐款不超 过500元 | 10 | ||
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,则θ1与θ2的大小关系是( )
如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,则θ1与θ2的大小关系是( )| A. | θ1=θ2 | B. | θ1>θ2 | C. | θ1<θ2 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com