

| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 60 | ||
| 捐款不超 过500元 | 10 | ||
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
分析 (Ⅰ)由频率分布直方图可知,在抽取的100人中,经济损失不超过4000元的有70人,经济损失超过4000元的有30人,求出K2,得到有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
(Ⅱ)由频率分布直方图可知抽到自身经济损失超过4000元居民的频率为0.3,将频率视为概率.由题意知ξ的取值可能有0,1,2,3,且ξ~B(3,$\frac{3}{10}$).由此能求出ξ的分布列,期望E(ξ)和方差D(ξ).
解答 解:(Ⅰ)由频率分布直方图可知,在抽取的100人中,经济损失不超过4000元的有70人,经济损失超过4000元的有30人,则表格数据如下
| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 60 | 20 | 80 |
| 捐款不超 过500元 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{343}{1000}$ | $\frac{441}{1000}$ | $\frac{189}{1000}$ | $\frac{27}{1000}$ |
点评 本题考查离散型随机变量的分布列,期望和方差的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
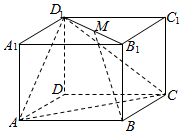 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 80 | |
| 女学生 | |||
| 总计 | 70 | 30 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com