
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 80 | |
| 女学生 | |||
| 总计 | 70 | 30 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 (1)列出2×2列联表,求出K2的值,判断有95%的把握认为“男学生和女学生喜欢古典音乐的程度有差异”;
(2)先确定X的取值,分别求其概率,求出分布列和数学期望.
解答 解:(1)2×2列联表
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 20 | 80 |
| 女学生 | 10 | 10 | 20 |
| 总计 | 70 | 30 | 100 |
| X | 3 | 4 | 5 |
| P | $\frac{2}{9}$ | $\frac{5}{9}$ | $\frac{2}{9}$ |
点评 本题考查概率的计算,考查独立性检验知识,求X的分布列及数学期望,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{e}$,-$\frac{4}{{e}^{2}}$] | B. | [-$\frac{2}{e}$,2e] | C. | [-$\frac{4}{{e}^{2}}$,2e] | D. | [$\frac{4}{{e}^{2}}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 60 | ||
| 捐款不超 过500元 | 10 | ||
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
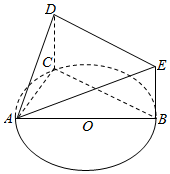 如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.
如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,则θ1与θ2的大小关系是( )
如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,则θ1与θ2的大小关系是( )| A. | θ1=θ2 | B. | θ1>θ2 | C. | θ1<θ2 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.若△ABD的面积为7,则AB=$\sqrt{37}$.
如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.若△ABD的面积为7,则AB=$\sqrt{37}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com