
 如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,则θ1与θ2的大小关系是( )
如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,则θ1与θ2的大小关系是( )| A. | θ1=θ2 | B. | θ1>θ2 | C. | θ1<θ2 | D. | 不能确定 |
分析 作AO⊥平面BCD,垂足是O,连接CO,过点C作直线l∥MN,在l上取点H,令CH=CO,在△AOC和△AHC中,CO=CH,AO⊥平面BCD,从而AO<AH,由此能求出θ1<θ2.
解答 解:作AO⊥平面BCD,垂足是O,连接C
过点C作直线l∥MN,在l上取点H,令CH=CO,
在△AOC和△AHC中,CO=CH,AO⊥平面BCD,
∴AO<AH,
∴∠ACO<∠ACH,
∵AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,
AO⊥平面BCD,CH∥MN,
∴∠ACO=θ1,∠ACH=θ2,
∴θ1<θ2.
故选:C.
点评 本题考查直线与平面所成的角和直线与直线所成的角的大小关系的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
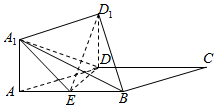 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
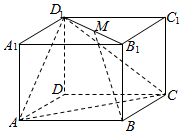 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=3,M是线段B1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 80 | |
| 女学生 | |||
| 总计 | 70 | 30 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com