
分析 (1)根据向量平行与坐标的关系列方程解出x,得出$\overrightarrow{a},\overrightarrow{b}$的坐标,再计算$\overrightarrow{a}-\overrightarrow{b}$的坐标,再计算|$\overrightarrow{a}-\overrightarrow{b}$|;
(2)令$\overrightarrow{a}•\overrightarrow{b}>0$得出x的范围,再去掉$\overrightarrow{a},\overrightarrow{b}$同向的情况即可.
解答 解:(1)∵$\overrightarrow{a}∥\overrightarrow{b}$,∴-x-x(2x+3)=0,解得x=0或x=-2.
当x=0时,$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(3,0),∴$\overrightarrow{a}-\overrightarrow{b}$=(-2,0),∴|$\overrightarrow{a}-\overrightarrow{b}$|=2.
当x=-2时,$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(-1,2),∴$\overrightarrow{a}-\overrightarrow{b}$=(2,-4),∴|$\overrightarrow{a}-\overrightarrow{b}$|=2$\sqrt{5}$.
综上,|$\overrightarrow{a}-\overrightarrow{b}$|=2或2$\sqrt{5}$.
(2)∵$\overrightarrow{a}$与$\overrightarrow{b}$夹角为锐角,∴$\overrightarrow{a}•\overrightarrow{b}>0$,
∴2x+3-x2>0,解得-1<x<3.
又当x=0时,$\overrightarrow{a}∥\overrightarrow{b}$,
∴x的取值范围是(-1,0)∪(0,3).
点评 本题考查了平面向量的坐标运算,数量积运算,向量平行与坐标的关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
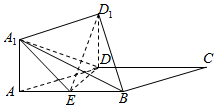 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,l∥β,则 α∥β | B. | 若l∥α,l⊥β,则α⊥β | ||
| C. | 若α⊥β,l⊥α,则 l⊥β | D. | 若α⊥β,l∥α,则l⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 总计 | |
| 男学生 | 60 | 80 | |
| 女学生 | |||
| 总计 | 70 | 30 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com