
分析 (I)由椭圆性质可知$|{{M}F}|=\frac{c}{a}({\frac{a^2}{c}-{x_{M}}})=a-\frac{c}{a}{x_{M}}$,其中c>0,c2=a2-b2,又x M∈[-a,a],故|MF|∈[a-c,a+c],则$\left\{\begin{array}{l}a+c=3+\sqrt{5}\\ a-c=3-\sqrt{5}\end{array}\right.$,解之得a,c的值,进一步得到椭圆T的方程.
(II)由题知直线AB的方程为$y=\frac{2}{3}x+2$,设直线l:$y=\frac{2}{3}x+m$与椭圆T相切于x轴下方的点M0,则△ABM0的面积为△ABM的面积的最大值S0,联立直线和椭圆方程即可求得m的值,再求出直线AB与直线l距离,则△ABM的面积的最大值可求.
解答 解:(I)由椭圆性质可知$|{{M}F}|=\frac{c}{a}({\frac{a^2}{c}-{x_{M}}})=a-\frac{c}{a}{x_{M}}$,其中c>0,c2=a2-b2,
∵x M∈[-a,a],故|MF|∈[a-c,a+c],则$\left\{\begin{array}{l}a+c=3+\sqrt{5}\\ a-c=3-\sqrt{5}\end{array}\right.$,解之得$\left\{\begin{array}{l}a=3\\ c=\sqrt{5}\end{array}\right.$.
故b2=a2-c2=4,椭圆T的方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$.
(II)由题知直线AB的方程为$y=\frac{2}{3}x+2$,设直线l:$y=\frac{2}{3}x+m$与椭圆T相切于x轴下方的点M0(如上图所示),则△ABM0的面积为△ABM的面积的最大值S0.
则$\left\{\begin{array}{l}{y=\frac{2}{3}x+m}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1}\end{array}\right.$即$\frac{2}{9}{x}^{2}+\frac{m}{3}x+\frac{{m}^{2}}{4}-1=0$,则$△=\frac{{m}^{2}}{9}-4×\frac{2}{9}(\frac{{m}^{2}}{4}-1)=0$解得m=$-2\sqrt{2}$.
此时,直线AB与直线l距离为$\frac{{2+2\sqrt{2}}}{{\sqrt{1+\frac{4}{9}}}}=\frac{{3({2+2\sqrt{2}})}}{{\sqrt{13}}}$,而$|{{A}{B}}|=\sqrt{13}$,${S_0}=\frac{1}{2}•\sqrt{13}•\frac{{3({2+2\sqrt{2}})}}{{\sqrt{13}}}=3({1+\sqrt{2}})$.
∴△ABM的面积的最大值是$3(1+\sqrt{2})$.
点评 本题考查了椭圆的简单性质,考查了点到直线的距离公式,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{15}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{13}}}{3}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
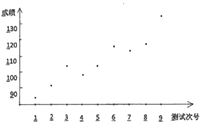 对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如图散点图.下面关于这位同学的数学成绩的分析中,正确的共有( )个
对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如图散点图.下面关于这位同学的数学成绩的分析中,正确的共有( )个| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 60 | ||
| 捐款不超 过500元 | 10 | ||
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com