
| A. | 若l∥α,l∥β,则 α∥β | B. | 若l∥α,l⊥β,则α⊥β | ||
| C. | 若α⊥β,l⊥α,则 l⊥β | D. | 若α⊥β,l∥α,则l⊥β |
分析 对4个选项分别进行判断,即可得出结论.
解答 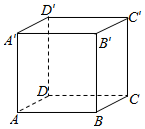 解:若l∥α,l∥β,则 α∥β或α,β相交,故A不正确;
解:若l∥α,l∥β,则 α∥β或α,β相交,故A不正确;
根据线面平行的性质可得:若l∥α,经过l的直线与α的交线为m,则l∥m,∵l⊥β,∴m⊥β,根据平面与平面垂直的判定定理,可得α⊥β,故B正确;
若l⊥α,α⊥β,则l?β或l∥β,故C错误;
作出正方体ABCD-A′B′C′D′,设平面ABCD为α,ADD′A′为β,则α⊥β,
观察正方体,得到:B′C′∥α,且B′C′∥β;A′D′∥α,且A′D′?β;A′B′∥α,且A′B′与β相交.∴面α、β及直线l满足:α⊥β,l∥α,则一定有l∥β或l?β或l与β相交,故D不正确.
故选:B.
点评 “由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (2,3) | C. | (1,2) | D. | ($\sqrt{5}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
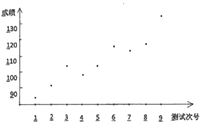 对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如图散点图.下面关于这位同学的数学成绩的分析中,正确的共有( )个
对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如图散点图.下面关于这位同学的数学成绩的分析中,正确的共有( )个| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{e}$,-$\frac{4}{{e}^{2}}$] | B. | [-$\frac{2}{e}$,2e] | C. | [-$\frac{4}{{e}^{2}}$,2e] | D. | [$\frac{4}{{e}^{2}}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com