
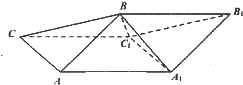
 斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.
斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.分析 (1)要证:AA1⊥BC1,先说明△AA1B是等边三角形,设D是AA1的中点、连接BD,C1D,证明AA1⊥平面BC1D,即可.
(2)求该斜三棱柱的体积,转化为直截面的面积和高的积,即可求解.
解答  (1)证明:由题意△AA1B是等边三角形.(2分)
(1)证明:由题意△AA1B是等边三角形.(2分)
设D是AA1的中点、连接BD,C1D,
则BD⊥AA1,
由四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角,可得∠AA1C1=60°,
所以△AA1C1是等边三角形,
且C1D⊥AA1,所以AA1⊥平面BC1D.(6分)
又BC1?平面BC1D,故AA1⊥BC1.(7分)
(2)解:由(1)知AA1⊥平面BC1D(9分),
由(1)知BD⊥AA1,又侧面ABB1A1⊥侧面AA1C1C,
所以BD⊥平面AA1C1C,
即BD⊥BC1,
△BC1D中,BD=BC1=$\sqrt{3}$,${S}_{△B{C}_{1}D}$=$\frac{1}{2}×\sqrt{3}×\sqrt{3}$=$\frac{3}{2}$(13分)
故该斜三棱柱的体积为$\frac{3}{2}×2$=3.(14分)
点评 本题考查直线与平面的垂直,棱锥的体积,考查空间想象能力,逻辑思维能力,是中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ②③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
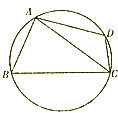 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
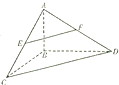 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
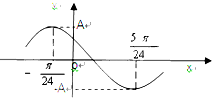 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )| A. | -$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com