
分析 (Ⅰ)用指数函数、反比例函数的单调性可作出判断;
(Ⅱ)先设f(x)为奇函数,然后根据奇函数性质可得f(-x)=-f(x),由此求得a值.
解答 解:(Ⅰ)∵y=2x单调递增,
∴y=$\frac{2}{{{2^x}+1}}$单调递减,y=-$\frac{2}{{{2^x}+1}}$单调递增,
∴f(x)=a-$\frac{2}{{{2^x}+1}}$单调递增;
(Ⅱ)若f(x)是奇函数,则f(-x)=-f(x),
∴a-$\frac{2}{{2}^{-x}+1}$=-(a-$\frac{2}{{{2^x}+1}}$),即2a=$\frac{2}{{{2^x}+1}}$+$\frac{2}{{2}^{-x}+1}$=$\frac{2}{{{2^x}+1}}$+$\frac{2•{2}^{x}}{1+{2}^{x}}$=2,
∴a=1,
故存在实数a=1使f(x)为奇函数.
点评 本题考查函数奇偶性、单调性的判断,属基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{15}{32}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2sinx | B. | f(x)=2cosx | C. | f(x)=cos2x | D. | f(x)=sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2x | B. | -3x | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
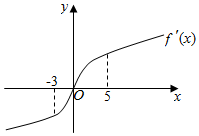
| A. | (-3,0) | B. | (-3,5) | C. | (0,5) | D. | (-∞,-3)∪(5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥3 | B. | a≤-3 | C. | a<-3 | D. | a>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p为真 | B. | ¬q为假 | C. | p∧q为真 | D. | p∨q为假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com