练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

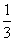    已知曲线y＝x3＋.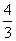

    (1)求曲线在点P(2,4)处的切线方程；

    (2)求曲线过点P(2,4)的切线方程．


    y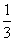＝x3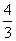＋，则y′＝x2.

    (1)由题意可知点P(2,4)为切点，

    y′|x＝2＝22＝4，

    所以曲线在点P(2,4)处的切线方程为y－4＝4(x－2)，即4x－y－4＝0.

    (2)由题意可知点P(2,4)不一定为切点，故设切点为(x0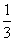，x＋)，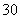

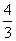    y′|x＝x0＝x，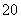

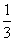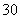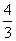    曲线过点P(2,4)的切线方程为y－(x＋)＝x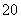(x－x0)，

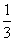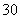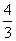    所以4－(x＋)＝x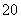(2－x0)，

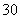    x－3x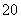＋4＝0⇔(x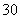＋1)－3(x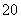－1)＝0⇔(x0＋1)(x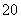－4x0＋4)＝0.

    解得x0＝－1或x0＝2，

    即切点为(－1,1)或(2,4)．

    所以曲线过点P(2,4)的切线方程为x－y＋2＝0或4x－y－4＝0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    将正奇数排列如下表，其中第i行第j个数表示aij(i∈N*，j∈N*)，例如a32＝9，若aij＝2 009，则i＋j＝________________.

    　　　　　　　　　　1

    　　　　　　　　　3　5

    　　　　　　　　7　9　11

    　　　　　　　13　15　17　19

    　　　　　　　　　 …

    查看答案和解析>>

    科目：高中数学 来源： 题型：


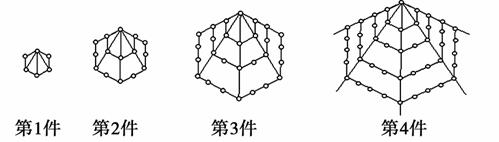
    一次展览会上展出一套由宝石串联制成的工艺品，如图所示．若按照这种规律依次增加一定数量的宝石，则第5件工艺品所用的宝石数为______颗；第n件工艺品所用的宝石数为______________颗(结果用n表示)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝2x＋lnx，且f ′(a)＝0，则2aln2a＝(　　)

    A．1                                                             B．－1

    C．－ln2                                                       D．ln2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若曲线y＝kx＋lnx在点(1，k)处的切线平行于x轴，则k＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若曲线f(x)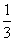＝ax3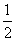＋bx2＋cx＋d(a，b，c>0)上存在斜率为0的切线，则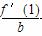－1的取值范围是(　　)

    A．(1，＋∞)                                                B．[1，＋∞)

    C．(2，＋∞)                                                D．[2，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求下列函数的导数：

    y＝3xex－2x＋e；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3－2x2－4x－7，其导函数为f ′(x)．则以下四个命题：

    ①f(x)的单调减区间是(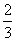，2)；

    ②f(x)的极小值是－15；

    ③当a>2时，对任意的x>2且x≠a，恒有f(x)>f(a)＋f ′(a)(x－a)；

    ④函数f(x)有且只有一个零点．

    其中真命题的个数为(　　)

    A．1个                                                         B．2个

    C．3个                                                         D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)的定义域为[－3，＋∞)，且f(6)＝2.f ′(x)为f(x)的导函数，f ′(x)的图象如图所示．若正数a，b满足f(2a＋b)<2，则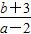的取值范围是(　　)

    A．(－∞，－)∪(3，＋∞)

    B．(－，3)

    C．(－∞，－)∪(3，＋∞)

    D．(－，3)

    查看答案和解析>>

    同步练习册答案