
| A. | (-3,0)∪(2,3) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(2,+∞) |
分析 由(x-2)•f(x)<0对x>0或x<0进行讨论,把不等式(x-2)•f(x)<0转化为f(x)>0或f(x)<0的问题解决,根据f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,把函数值不等式转化为自变量不等式,求得结果.
解答 解:∵f(x)是R上的奇函数,且在(0,+∞)内是增函数,
∴在(-∞,0)内f(x)也是增函数,
又∵f(-3)=0,
∴f(3)=0
∴当x∈(-∞,-3)∪(0,3)时,f(x)<0;当x∈(-3,0)∪(3,+∞)时,f(x)>0;
∴(x-2)•f(x)<0的解集是(-3,0)∪(2,3)
故选:A.
点评 考查函数的奇偶性和单调性解不等式,体现了分类讨论的思想方法,属基础题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,$lgx+\frac{1}{lgx}≥2$ | B. | 当x>0时,$\sqrt{x}+\frac{1}{{\sqrt{x}}}≥2$ | ||
| C. | 当x≥2时,$x+\frac{1}{x}≥2$ | D. | 当0<x≤2时,$x-\frac{1}{x}$无最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
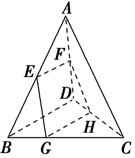 如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2,求证:
如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\frac{{\sqrt{19}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {x|-1≤x≤1} | C. | {-1,0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,2) | C. | (3,+∞) | D. | (-∞,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com