
���� ֱ�����÷������ԭ�������ɵó����ۣ�
��� �⣺�������ԭ�������һ���£���n��취���ڵ�1��취����m1�ֲ�ͬ�ķ������ڵ�2��취����m2�ֲ�ͬ�ķ��������ڵ�n��취����mn�ֲ�ͬ�ķ�������ô�������¹��У�N=m1+m2+��+mn�ֲ�ͬ�ķ�����
��1����ɴ��������ȡһ���飬ÿȡһ���������������£������÷������ԭ��������
��2�����������ȡ�����飬������ѧ�飬�����飬Ӣ�����һ��������������Ҫ3���������÷ֲ�����ԭ��������
��3����ɵص��ҵأ���3��취��ÿһ���а취�����������£������÷������ԭ��������
�ʴ�Ϊ����1����3����
���� ������Ҫ�����˷������ԭ�����������ԭ���ǣ���һ�����飬�������n��취���ڵ�һ��취����m1�ֲ�ͬ�ķ������ڵڶ���취����m2�ֲ�ͬ�ķ����������ڵ�n��취����mn�ֲ�ͬ�ķ�������ô���������鹲��m1+m2+��+mn�ֲ�ͬ�ķ������˷�ԭ���ǣ�����һ���£��������Ҫ�ֳ�n�����裬����һ����m1�ֲ�ͬ�ķ��������ڶ�����m2��ͬ�ķ�������������n����mn��ͬ�ķ�������ô�������¹��� N=m1��m2������mn�ֲ�ͬ�ķ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
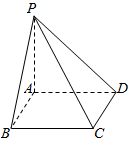 ��ͼ��������P-ABCD�У�����ABCD�DZ߳�Ϊa�������Σ�PA��ƽ��ABCD����PA=a����ֱ��PB��ƽ��PCD���ɵĽǵĴ�СΪ$\frac{��}{6}$��
��ͼ��������P-ABCD�У�����ABCD�DZ߳�Ϊa�������Σ�PA��ƽ��ABCD����PA=a����ֱ��PB��ƽ��PCD���ɵĽǵĴ�СΪ$\frac{��}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1]��[3��+�ޣ� | B�� | ��-�ޣ�1] | C�� | [3��+�ޣ� | D�� | [$\frac{3}{2}$��$\frac{11}{6}}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com