
分析 利用D为BC的中点,求出$\overrightarrow{OD}$,从而求出$\overrightarrow{AD}$即可.
解答 解:在四面体O-ABC中,$\overrightarrow{OA}=\overrightarrow a$,$\overrightarrow{OB}=\overrightarrow b$,$\overrightarrow{OC}=\overrightarrow c$,D为BC的中点,
∴$\overrightarrow{OD}$=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)=$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$,
∴$\overrightarrow{AD}$=$\overrightarrow{OD}$-$\overrightarrow{OA}$=$\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c-\overrightarrow a$,
故答案为:$\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c-\overrightarrow a$.
点评 本题考查向量中点公式的应用,以及两个向量的加减法的法则和几何意义.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
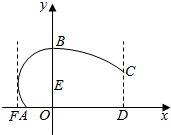 某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).
某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com