
分析 令g(x)=x2f(x),讨论x>1,0<x<1时,g(x)的单调区间和极值点,可得g′(1)=0,即有2f(1)+f′(1)=0,由f′(1)=-$\frac{3}{4}$,即可得出.
解答 解:当x>0且x≠1时,$\frac{2f(x)+xf′(x)}{x-1}$>0,
可得:x>1时,2f(x)+xf′(x)>0;1>x>0时,2f(x)+xf′(x)<0.
令g(x)=x2f(x),x∈(0,+∞).
∴g′(x)=2xf(x)+x2f′(x)=x[2f(x)+xf′(x)].
可得:x>1时,g′(x)>0;1>x>0时,g′(x)<0.
可得:函数g(x)在x=1处取得极值,
∴g′(1)=2f(1)+f′(1)=0,f′(1)=-$\frac{3}{4}$,
∴f(1)=$-\frac{1}{2}×(-\frac{3}{4})$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 本题考查了利用导数研究函数的单调性极值及其切线斜率,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②⑤ | B. | ①②④ | C. | ②③④ | D. | ③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R2的取值越小,模型拟合效果越好 | |
| B. | R2的取值可以任意大,且R2取值越大,拟合效果越好 | |
| C. | R2的取值越接近于1,模型拟合效果越好 | |
| D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
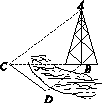 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB| A. | 10$\sqrt{2}$ m | B. | 10$\sqrt{3}$ m | C. | 15$\sqrt{6}$ m | D. | 10$\sqrt{6}$ m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥-1 | B. | a≥-2 | C. | a≥2 | D. | a≥3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com