
| A. | e${\;}^{{x}^{4}-{x}^{3}}$-1 | B. | cosx2-1 | C. | $\sqrt{1+{x}^{2}}$-1 | D. | tanx-sinx |
分析 根据无穷小阶数的定义,若$\underset{lim}{x→0}$$\frac{f(x)}{x^n}$=c(c≠0),则f(x)为n阶无穷小量,再逐个确定各个函数的阶数.
解答 解:根据无穷小阶数的定义,若$\underset{lim}{x→0}$$\frac{f(x)}{x^n}$=c(c≠0),则f(x)为n阶无穷小量,
对于A:$\underset{lim}{x→0}$$\frac{{e}^{x^4-x^3}-1}{x^3}$=$\underset{lim}{x→0}$$\frac{x^2(4x-3)•{e}^{x^4-x^3}}{3x^2}$=$\underset{lim}{x→0}$$\frac{(4x-3){e}^{x^4-x^3}}{3}$=-1,
所以A选项的阶数是3;
对于B:$\underset{lim}{x→0}$$\frac{cosx^2-1}{x^4}$=-$\underset{lim}{x→0}$$\frac{2x•sinx^2}{4x^3}$=-$\underset{lim}{x→0}$$\frac{sinx^2}{2x^2}$=-$\frac{1}{2}$,
所以B选项的阶数是4;
对于C:$\underset{lim}{x→0}$$\frac{\sqrt{1+x^2}-1}{x^2}$=$\underset{lim}{x→0}$$\frac{1}{\sqrt{1+x^2}+1}$=$\frac{1}{2}$,
所以C选项的阶数是2;
对于D:$\underset{lim}{x→0}$$\frac{tanx-sinx}{x^3}$=$\underset{lim}{x→0}$$\frac{1-cos^3x}{3x^2cos^2x}$=$\underset{lim}{x→0}$=$\frac{1}{2}$•$\underset{lim}{x→0}$$\frac{sinx•cos^2x}{x•(cos^2x+xsinxcosx)}$=$\frac{1}{2}$,
所以D选项的阶数是3;
因此,阶数最高的是B选项,故选B.
点评 本题主要考查了极限及其运算,涉及无穷小量阶数的求解,以及运用洛必达法则求函数极限,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:选择题
| A. | y=100×0.01210 | B. | y=100×(1+1.2%)10 | C. | y=100×(1-1.2%)10 | D. | y=100×1.210 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(cm) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 49 | 46 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(cm) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y(码) | 42 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
| 高个 | 非高个 | 合计 | |
| 大脚 | |||
| 非大脚 | 12 | ||
| 合计 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
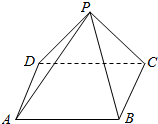 已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com