
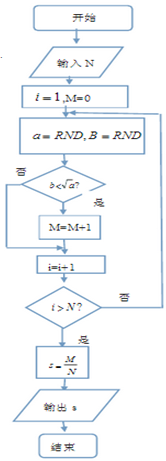
 在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是
在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是| a |
| a |
| a |
| ∫ | 1 0 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |


科目:高中数学 来源: 题型:
| an+1 |
| an-1 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| A、①② | B、③④ | C、①③ | D、②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com