解:(1)∵函数f(x)=ax
3+bx
2+cx(a≠0,x∈R)为奇函数,∴f(-x)=-f(x),
∴-ax
3+bx
2-cx=-(ax
3+bx
2+cx)
∴b=0
∵在x=1处取得极值2,∴
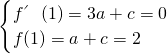
,
∴a=-1,c=3,
∴f(x)=-x
3+3x;
(2)g(x)=-x
2+3+(k+1)lnx,∴
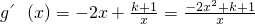
当k<-1时,g′(x)<0,所以在(0,+∞)递减;
当k=-1时,g′(x)≤0,所以在(0,+∞)递减;
当k>-1时,在
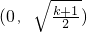
时,g′(x)>0,g(x)递增;在

,g′(x)<0,g(x)递增.
(3)根据题意f(x)
min≥h(x)
min,f′(x)=-3x
2+3=-3(x+1)(x-1)
所以x∈[-2,-1]递减,x∈[-1,1]递增,于是当x=1时,f(x)的最小值为-2
当b>2时,f(x)
min=-2≥h(x)
min=8-4b,所以
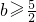
;
当1≤b≤2时,
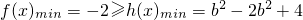
,所以
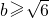
或
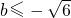
(舍去)
当b<1,f(x)
min=-2≥h(x)
min=h(1)=1-2b+4=5-2b,所以
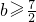
(舍去)
所以
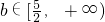
.
分析:(1)利用函数f(x)=ax
3+bx
2+cx(a≠0,x∈R)为奇函数,可得b=0,利用在x=1处取得极值2,可得a=-1,c=3,从而可得y=f(x)的解析式;
(2)求导函数,分类讨论,利用导数的正负,可得函数的单调区间;
(3)根据题意f(x)
min≥h(x)
min,分类讨论,确定函数的最小值,解不等式,即可求b的取值范围.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,正确运用导数是关键.

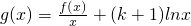 ,求函数y=g(x)的单调区间;
,求函数y=g(x)的单调区间;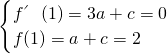 ,
,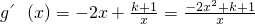
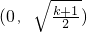 时,g′(x)>0,g(x)递增;在
时,g′(x)>0,g(x)递增;在 ,g′(x)<0,g(x)递增.
,g′(x)<0,g(x)递增.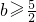 ;
;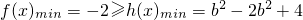 ,所以
,所以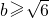 或
或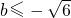 (舍去)
(舍去)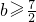 (舍去)
(舍去)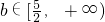 .
.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案